 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вычисление пределов
Предел элементарной функции в точке области ее определения равен частному значению функции в этой точке: 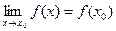 . Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводят к неопределенностям вида:
. Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводят к неопределенностям вида: 

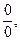
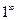 ,
, 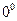 ,
, 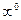 .
.
Элементарными приемами раскрытия неопределенностей являются: 1) сокращение на множитель, создающий неопределенность; 2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при  ); 3) применение эквивалентных функций; 4) использование двух замечательных пределов:
); 3) применение эквивалентных функций; 4) использование двух замечательных пределов:
а) 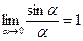 ;
;
b) 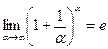 или
или  .
.
С учетом использования эквивалентных бесконечно малых функций, можно привести другие формы записи выражения первого замечательного предела:
 .
.
Для второго замечательного предела на практике целесообразно использовать соотношения:
1) 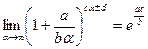 ;
;
2) 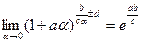 .
.
Пусть С - произвольная постоянная величина, 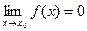 и
и 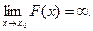 Тогда имеют место следующие соотношения:
Тогда имеют место следующие соотношения:
1) 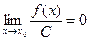 ; 2)
; 2) 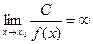 ;
;
3) 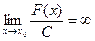 ; 4)
; 4)  ;
;
5) 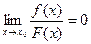 ; 6)
; 6)  .
.
П р и м ер. Найти 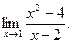
Решение:
Подставляя вместо переменной ее предельное значение и используя свойства пределов, получим: 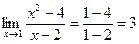 .
.
Ответ: 3.
П р и м е р. Найти 
Решение:
Непосредственная подстановка предельного значения переменной в выражение функции под знаком предела приводит к неопределенности вида 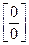 . Преображаем функцию, разложив числитель и знаменатель на множители:
. Преображаем функцию, разложив числитель и знаменатель на множители:
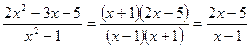 .
.
Найдем предел функции после преобразования:
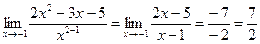 .
.
Ответ: 
П р и м е р. Найти  .
.
Решение:
Непосредственная подстановка значения переменной 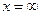 в выражение функции под знаком предела приводит к неопределенности вида
в выражение функции под знаком предела приводит к неопределенности вида 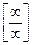 . Разделим числитель и знаменатель дроби на x 2. Получим:
. Разделим числитель и знаменатель дроби на x 2. Получим:
 .
.
Но 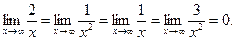
Тогда 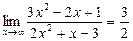 .
.
Ответ:  .
.
Можно показать, что предел отношения двух многочленов на бесконечности равен отношению коэффициентов старших членов, если в числителе и знаменателе будут многочлены одной степени. Этот же предел будет равен 0, если степень многочлена в числителе будет меньше степени многочлена в знаменателе, и будет равен 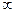 , если степень многочлена в числителе будет выше степени многочлена в знаменателе.
, если степень многочлена в числителе будет выше степени многочлена в знаменателе.
П р и м е р. Найти  .
.
Решение:
Непосредственная подстановка предельного значения переменной в выражении функции под знаком предела приводит к неопределенности вида 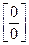 . Преобразуем функцию следующим образом:
. Преобразуем функцию следующим образом:
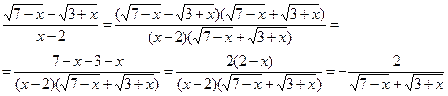
Найдем предел функции после преобразования:
 .
.
П р и м е р. Найти 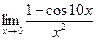 .
.
Решение:
Непосредственная подстановка предельного значения в выражение функции под знаком предела приводит к неопределенности вида 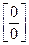 . Преобразуем функцию следующим образом:
. Преобразуем функцию следующим образом: 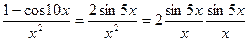 . Тогда
. Тогда 
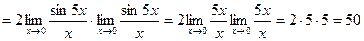 .
.
Ответ: 50.
П р и м е р. Вычислить 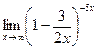 .
.
Решение:
Непосредственная подстановка предельного значения переменной в функцию под знаком предела приводит к неопределенности вида 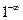 . Воспользуемся выражением второго замечательного предела в виде:
. Воспользуемся выражением второго замечательного предела в виде: 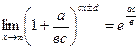 .
.
Получим: 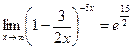 .
.
Ответ:  .
.
Можно получить более общее выражение для вычисления пределов такого типа: 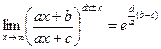 (справедливость этого соотношения доказать самостоятельно).
(справедливость этого соотношения доказать самостоятельно).
Поиск по сайту: