Парабола

Определение. Параболой называется геометрическое место точек плоскости, расстояние от каждой из которых к фиксированной точке плоскости будет равно расстоянию к прямой, называемой директрисой.

Основными характеристиками параболы являются вершина С (а; в), параметр 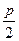и направление веток параболы. Параметр 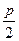определяет расстояние от вершины параболы к фокусу и директрисе. Каноническое уравнение параболы выражается одним из уравнений:

Знак в этих соотношениях определяет направление веток параболы. Если вершину параболы поместить в точку О (0;0), то каноническое уравнение параболы будет выражаться одним из соотношений:

у ²=±2 рх или х ²=±2 ру.

Задача. Найти основные характеристики и построить параболу, заданную уравнением: х ²-4 х -8 у -4=0.

Решение:

Преобразуем уравнение параболы к каноническому виду:

(х -2)²-4-8 у -4=0,

(х -2)²=8 у +8,

(х -2)²=8(у +1).

Сравнивая полученное уравнение с каноническим уравнением параболы в общем виде, определяем ее характеристики.

Вершина параболы будет находится в точке С (2;-1), параметр р будет равен 4, а ветви параболы будут иметь положительное направление оси Оу.

Построим параболу.

у

1 F

-1 1 2 3 4 5 х

-1 С у =-1

Если при построении графика кривой второго порядка определенного вида предполагается использование вычислительной техники, то часто бывает целесообразным переход от декартовой прямоугольной к полярной системе координат r = f (a).

Задача. Составить уравнение геометрического места точек, отношение расстояний от каждой из которых к точке F (4;0) и прямой х =10 равно 1/2.

Решение:

Пусть М (х;у) - произвольная точка искомой линии. Тогда расстояние будет равно:

.

Расстояние d ₂ от точки М (х; у) и прямой х =10 будет равно расстоянию | ВМ |, где В (10; у) будет основой перпендикуляра проведенного из точки М (х; у) на прямую х =10.

.

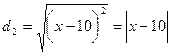По условию задачи , d ₂=2 d ₁,

,

(х -10)²=4(х -4)²+4 у ²,

3 х ²-12 х +4 у ²=36,

3(х ²-4 х +4-4)+4 у ²=36,

3[(х -2)²-4]+4 у ²=36,

3(х -2)²-12+4 у ²=36,

3(х -2)²+4 у ²=48,

.

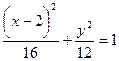Полученное уравнение является уравнением эллипса с полуосями а =4, в =2 , центром симметрии в точке О ₁(2;0) и фокусами F (4;0) и О (0;0)= F ₁.

Построим схематически чертеж эллипса .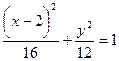

у

А ₁ А х

Поиск по сайту: