Расстояние от точки до прямой

Расстояние от точки М₀(х₀;у₀) к прямой, заданной уравнением Ах+Ву+С =0, определяется соотношением:

.

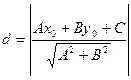Задача 3. Найти условия параллельности прямых, угловые коэффициенты которых равны, соответственно, к ₁ и к ₂.

Решение:

Воспользуемся соотношением 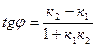, выражающим тангенс угла, образованного прямыми l ₁ и l ₂. Если l ₁êê l ₂, то в этом случае j =0 и tgj =0. Тогда получим: .

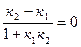к₁=к₂ - условие параллельности прямых

Ответ: к₁=к₂.

Аналогично можно получить соотношение 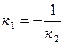- выражающее условие перпендикулярности прямых l ₁ и l ₂.

Задача 4. Найти угол между прямыми 2 х +3 у -6=0 и х -2 у +4=0.

Решение:

Пусть l ₁: 2 х +3 у -6=0 и l ₂: х -2 у +4=0.

Найдем угловой коэффициент прямой l ₁: .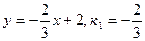

Найдем угловой коэффициент прямой l ₂: .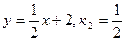

Воспользуемся соотношением: .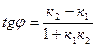

.

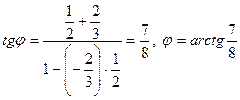Ответ: .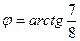

Задача 5. Составить уравнение прямой, проходящей через точки А (2;-3) и В (-1;4).

Решение:

Воспользуемся соотношением .

Пусть х ₁=2, у ₁=-3, х ₂=-1, у ₂=4. Тогда получим:

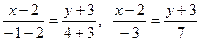- искомое уравнение прямой, проходящей через точки А и В.

Преобразуем это уравнение к другим видам.

7(х -2)=-3(у +3), 7 х +3 у -5=0 - общее уравнение прямой.

3 у =-7 х +5, 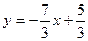- уравнение прямой с угловым коэффициентом.

7 х +3 у =5, 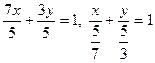- уравнение в отрезках на осях координат.

Задача 6. Составить уравнение прямой, проходящей через точку М (1;2), перпендикулярно прямой 2 х +3 у -1=0.

Решение:

Составим уравнение пучка прямых, проходящих через точку М: у -2= к (х -1). Найдем угловой коэффициент прямой 2 х +3 у -1=0:

.

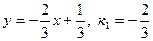Воспользуемся условием перпендикулярности прямых:

, .

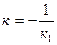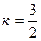Подставим значение 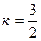в уравнение пучка прямых:

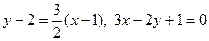- искомое уравнение прямой.

Задача 7. Найти расстояние от точки М (1;-2) к прямой

3 х - у +1=0.

Решение:

Воспользуемся соотношением: 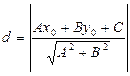, где А, В, С коэффициенты уравнения прямой 3 х - у +1=0, а х₀, у₀ - координаты точки М.

Получим:

.

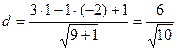Ответ: .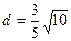

Поиск по сайту: