Задания для самостоятельной работы. Задание 1. Даны вершины А(х1;у1), В(х2;у2), С(х3;у3) треугольника АВС

Задание 1. Даны вершины А(х₁;у₁), В(х₂;у₂), С(х₃;у₃) треугольника АВС. Необходимо найти:

1) периметр D АВС;

2) систему неравенств, определяющих внутреннюю область D АВС;

3) сторону АВ, используя теорему косинусов и определяя косинус угла С его выражением через тангенс этого угла;

4) точку пересечения высот;

5) точку пересечения медиан;

6) уравнение биссектрисы угла А;

7) площадь D АВС;

8) точки Р ₁ и Р ₂, которые делят сторону АС на три равные части.

Задание 2. Найти площадь D А₁В₁С₁, где А₁, В₁, С₁ - точки, симметричные вершинам А, В, С относительно сторон ВС, АС и АВ. Задание выполнить с использованием ЭВМ. Координаты вершин треугольника заданы матрицей:

.

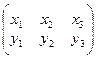№№ 4.1.1-4.1.20

4.1.1 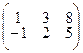; 4.1.2 ;

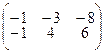4.1.3 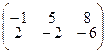; 4.1.4 ;

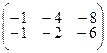4.1.5 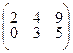; 4.1.6 ;

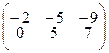4.1.7 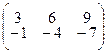; 4.1.8 ;

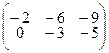4.1.9 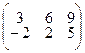; 4.1.10 ;

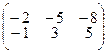4.1.11 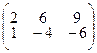; 4.1.12 ;

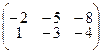4.1.13 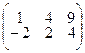; 4.1.14 ;

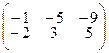4.1.15 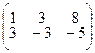; 4.1.16 ;

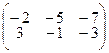4.1.17 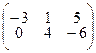; 4.1.18 ;

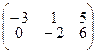4.1.19 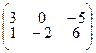; 4.1.20 .

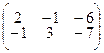Уравнение линии второго порядка на плоскости.

Простейшими кривыми второго порядка являются окружность, эллипс, гипербола и парабола.

Поиск по сайту: