АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Функция. Предел функции одной переменной

Читайте также:
  1. A) эффективное распределение ресурсов
  2. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  3. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  4. I. Определите тип придаточного предложения.
  5. I. Определите, какое из этих высказываний несет психологическую информацию.
  6. I. Открытые способы определения поставщика.
  7. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  8. II. Основные задачи и функции
  9. II. Прочтите слова и определите части речи( глаголы, существительные,
  10. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  11. II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ
  12. III. Определение оптимального уровня денежных средств.

Определение. Функцией называется закон, по которому каждому значению переменной величины х из множества , ставится в соответствие вполне определенное значение переменной величины у из множества .

Аналитически функциональная зависимость переменных х и у выражается соотношением .

Одним из важнейших понятий математического анализа является понятие предела функции.

Определение. Число А называется пределом функции f(x) в точке x = x 0, если для любой последовательности значений , существует последовательность значений .

Символически это записывается следующим образом: . Существует другое определение предела функции в точке.

Определение. Число А называется пределом функции f(x) в точке х = х 0, если для любого числа существует число такое, что для всех значений х, удовлетворяющих неравенству , выполняется неравенство .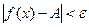

Понятие предела функции не учитывает значение функции в предельной точке, то есть величина 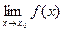не зависит от величины f(x0). Отсюда следует, что под знаком предела можно проводить тождественные преобразования аналитического выражения, задающего функцию, не принимая во внимание поведение функции в предельной точке.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)