 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Знакопеременные ряды
|
Читайте также: |
1. Ряд, у которого любые два соседних члена являются членами разных знаков, называют знакочередующимся.
Например, таким является ряд
 . (8)
. (8)
Знакочередующийся ряд записывают так:
 ап > 0.
ап > 0.
Одним из достаточных признаков сходимости знакочередующихся рядов является следующая теорема.
4. Теорема Лейбница. Если общий член знакочередующегося ряда, монотонно убывая по абсолютной величине, стремится к нулю, то ряд сходится.



 0 а2n a2n-1 a4 a3 a2 a1
0 а2n a2n-1 a4 a3 a2 a1

Ряд (8) по теореме Лейбница сходится, т.к. удовлетворяет условиям теоремы:
1)  ;
;
2) 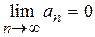 .
.
Действительно, 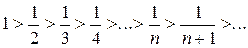 и
и  .
.
Следовательно, ряд (8) сходится.
Было установлено, что его сумма равна ln 2.
Пример 16. Исследовать на сходимость ряд  .
.
Решение. Ряд знакочередующийся, поэтому проверим выполнение условий теоремы Лейбница..
1) 
2)  .
.
Следовательно, данный ряд сходится.
Из теоремы Лейбница следует, что сумма всякого сходящегося знакочередующегося ряда с первым положительным членом всегда сама положительна и меньше этого первого члена, т.е.
 .
.
Если ряд сходится, то справедливо равенство:
 ,
,
где Sn - п -я частичная сумма ряда, а rn - остаток ряда (см.(6)).
По теореме 3 § 1 предел
 .
.
При достаточно большом номере п имеем: S» Sn.
Остаток знакочередующегося ряда является в свою очередь так же знакочередующимся рядом. Поэтому справедливо неравенство:
 .
.
Таким образом, при замене суммы знакочередующегося ряда, удовлетворяющего всем требованиям теоремы Лейбница, его п-ной частичной суммой, абсолютная погрешность не превосходит абсолютной величины первого отброшенного члена.
Отсюда следует, что знакочередующиеся ряды очень удобны для вычислительных целей.
Например, вычислим приближенно, с точностью до 0,01 сумму ряда:
 .
.
Для требуемой точности надо взять столько членов ряда, чтобы первый отбрасываемый член ряда был по модулю меньше 0,01. Тогда весь остаток ряда, которым пренебрегаем при вычислении суммы ряда, будет также меньше 0,01. Поэтому с точностью 0,01 получаем
 .
.
2. Обратимся теперь к вопросу о сходимости рядов, члены которых могут иметь произвольные знаки. Будем считать, что произвольные ряды имеют бесконечное число как положительных, так и отрицательных членов и расположение положительных и отрицательных членов в ряде совершенно произвольно.
5. Следует заметить, что знакочередующиеся ряды являются частным случаем таких произвольных рядов.
Рассмотрим произвольный числовой ряд
 (9)
(9)
и ряд, составленный из абсолютных членов ряда (9):
 . (10)
. (10)
Возможны следующие случаи:
а) ряды (9) и (10) одновременно сходятся;
б) ряд (9) сходится, а ряд (10) расходится.
Тогда в случае а) ряд (9) называют абсолютно сходящимся, а в случае б) ряд (9) называют условно сходящимся (неабсолютно сходящимся).
Следовательно, ряд (8) условно сходится, т.к. по теореме Лейбница он сходится, а ряд  , являющийся гармоническим, расходится.
, являющийся гармоническим, расходится.
Ряд, рассмотренный в примере является абсолютно сходящимся. Действительно, ряд, составленный из абсолютных величин примет вид:

и является суммой бесконечно убывающей геометрической прогрессии (см. (5)). Следовательно, ряд

сходится абсолютно.
Теорема 1. Из сходимости ряда (10) следует сходимость ряда (9).
Сформулируем ряд свойств, присущих только абсолютно сходящимся рядам.
Теорема 2. Абсолютно сходящиеся ряды обладают переместительным свойством.
Следовательно, в абсолютно сходящихся рядах сумма ряда не изменится при перестановке членов ряда.
Условно сходящиеся ряды этим свойством не обладают.
Риман показал, что сумму условно сходящегося ряда путем перестановки слагаемых можно сделать равной любому наперед заданному числу или даже получить расходящийся ряд.
Теорема 3. Для абсолютно сходящегося ряда (9) справедливо неравенство
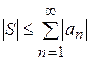 ,
,
где S =  .
.
Для абсолютно сходящихся рядов можно сформулировать один из достаточных признаков, например, признак Даламбера:
Теорема 4. Пусть дан ряд (9) и существует предел
 . (11)
. (11)
Тогда при D < 1 ряд (9) абсолютно сходится, а при D > 1 ряд (9) расходится.
Следует заметить, что при существовании предела (11) ряд (9) не может сходиться условно при D ¹ 1. Если же D = 1, то теорема 4 неприменима и в этом случае удобнее применять признаки сравнения для ряда (10).
Задание. Сформулируйте самостоятельно признак Коши абсолютной сходимости произвольных рядов.
Пример 17. Исследовать на сходимость следующие ряды:
а)  ; ;
| б)  ; ;
|
в) 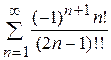 ; ;
| г)  . .
|
Решение. а) Составим ряд из абсолютных величин данного ряда
 . (12)
. (12)
Признак Даламбера не дает ответа, так как D = 1 (проверьте самостоятельно). Поэтому применим предельный признак сравнения (теорема 3 § 2) и сравним с расходящимся гармоническим рядом  (см. замечание 2 § 2). Тогда получим:
(см. замечание 2 § 2). Тогда получим:
 .
.
Следовательно, ряд (12) ведет себя так же, как и гармонический, т.е. расходится. Таким образом, данный ряд не является абсолютно сходящимся рядом.
Однако, заданный знакочередующийся ряд по теореме Лейбница сходится. Действительно, проверим неравенство 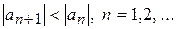
 ,
,
 ,
,
отсюда
 ,
,
или
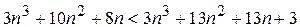 ,
,
или
 , которое выполняется для п = 1,2,3,....
, которое выполняется для п = 1,2,3,....
Кроме того,
 .
.
Следовательно, ряд  сходится условно.
сходится условно.
б) Рассмотрим ряд, составленный из абсолютных величин данного ряда
 .
.
Как и в предыдущем примере а) сравним этот ряд со сходящимся рядом  .
.
Получаем:
 .
.
Следовательно, ряд  сходится.
сходится.
Тогда по теореме 1 заданный ряд сходится, причем абсолютно.
Поиск по сайту: