 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Простейшие задачи на прямой
а) Расстояние между двумя точками.
Если имеются точки А(х1;у1) и В(х2;у2), то расстояние между ними определяется соотношением:
.
Если поместить один из концов отрезка в точку О (0;0), то длина отрезка в этом случае будет определятся соотношением:
,
где М(х;у) будет другой конечной точкой отрезка.
б) Деление отрезка в заданном отношении.
Говорят, что точка М делит отрезок АВ в отношении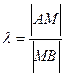 
, если известны координаты концов отрезка и параметр λ, то координаты точки М определяются следующим образом:
.
Если точка М - середина отрезка АВ, то соотношения примут вид:
- формулы деления
отрезка пополам
Формулы деления отрезка в заданном отношении также можно использовать для определения координат его концов:
.
Задача 1. Найти расстояние между точками А (3;1) и В (-5;-1).
Решение:
.
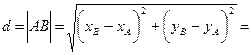
Ответ: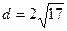 
.
Задача 2. Найти координаты точек М 1 и М 2, которые делят отрезок АВ на равные части, если точки А и В имеют координаты: А (2;5), В (-3;6).
Решение:
.
Используя значение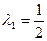 
, находим координаты точки М 1:
.
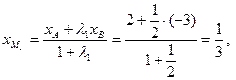
Таким образом М 1 
- первая искомая точка.
Для определения координат точки М 2 можно поступить аналогично, как и в случае точки М 1, с учетом того, что 
. Однако проще определить координаты точки М 2, как середины отрезка М1В:
.
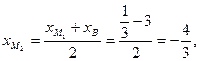
Ответ: М 1 , М 2 
.
Поиск по сайту: