 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Скалярного произведения
Задача 1. Найти выражение скалярного произведения векторов, заданных своими координатами.
Решение:
Пусть имеются векторы 
и 
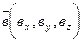. Тогда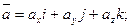 
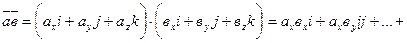
. Здесь использовалось то обстоятельство, что 
. Таким образом, 
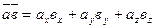выражение скалярного произведения в координатной форме.
Задача 2. Найти длину вектора .
Решение:
.
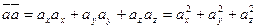С другой стороны: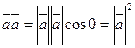 
.
Тогда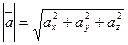 
- выражение для определения модуля вектора 
.
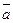Задача 3. Найти угол между векторами и .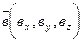
Решение:
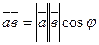. Преобразуем левую и правую часть равенства.
, 
.
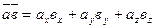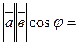
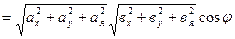Сравнивая правые части выражений, получим: 
- соотношение для определения угла между векторами.
Задача 4. Найти проекцию вектора 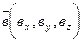на направление вектора .
Решение:
;
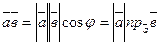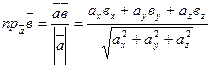- выражение проекции вектора 
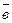на направление вектора .
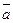Поиск по сайту: