 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Для векторного произведения можно написать формулу, аналогичную (4)
 ´
´ 
 = ê
= ê  ê×
ê×  ^
^ 
 ; (11)
; (11) 
здесь вектор  ^
^ 
 получается проектированием вектора
получается проектированием вектора  на плоскость, перпендикулярную к вектору
на плоскость, перпендикулярную к вектору  ,и последующим поворотом этой проекции в указанной плоскости на 90° против часовой стрелки (если смотреть со стороны вектора
,и последующим поворотом этой проекции в указанной плоскости на 90° против часовой стрелки (если смотреть со стороны вектора  ).
).
Если два вектора  и
и  коллинеарны, то
коллинеарны, то  ´
´  = 0. другие свойства таковы.
= 0. другие свойства таковы.
Свойства векторного произведения. 1)  ´
´  = -
= -  ´
´  ;2)
;2)  ´ k
´ k  = k
= k  ´
´  (k - число); 3)
(k - число); 3)  ´ (
´ ( +
+  ) =
) =  ´
´  +
+  ´
´  .
.
Свойства 2) и 3) получаются из формулы (11) и соответствующих свойств векторных проекций. Они означают, что при векторном умножении скобки раскрываются, как при умножении чисел. Например,(2  – 3
– 3  ) ´
) ´  = 2
= 2  ´
´  – 3
– 3  ´
´  . (Однако сочетательного свойства для
. (Однако сочетательного свойства для  ´(
´( ´
´  )нет.)
)нет.)
Из формулы (11) и определения легко вывести «таблицу» векторного умножения ортов 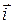 ,
,  ,
,  правой прямоугольной системы координат (далее рассматриваются правые системы):
правой прямоугольной системы координат (далее рассматриваются правые системы): 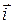 ´
´ 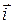 =
=  ´
´  =
=  ´
´  = 0;
= 0;
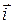 ´
´  =
=  ,
,  ´
´  =
= 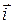 ,
,  ´
´ 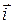 =
=  ;
;  ´
´ 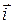 =-
=-  ,
,  ´
´  =-
=- 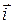 ,
, 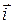 ´
´  =-
=-  .
.
Разлагая векторы  и
и  по ортам и используя «таблицу» векторного умножения ортов, получаем выражение для
по ортам и используя «таблицу» векторного умножения ортов, получаем выражение для  ´
´  , которое компактно записывается с помощью определителя (после раскрытия его получится вектор).
, которое компактно записывается с помощью определителя (после раскрытия его получится вектор).
Правило. Имеет место алгебраическая формула для векторного произведения векторов  (x 1; y 1; z 1)и
(x 1; y 1; z 1)и  (x 2; y 2; z 2):
(x 2; y 2; z 2):
 (12)
(12)
Поиск по сайту: