АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Смешанное произведение

Читайте также:
  1. III. Смешанное (квартирно-бивачное) размещение
  2. Автор - это гражданин, творческим трудом которого создано произведение.
  3. Векторное произведение.
  4. Воспроизведение.
  5. Договор об отчуждении исключительного права на произведение.
  6. Скалярное произведение.
  7. Смешанное вскармливание, его характеристика. Докорм.

Смешанное произведение трех геометрических векторов, обозначаемое как

(, , ) - это число ( ´ )× . Вначале вычисляется векторное произведение 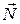= ´ , затем вектор 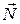умножается скалярно на вектор .

Геометрический смысл смешанного произведения: абсолютная величина смешанного произведения равна объему параллелепипеда, построенного на векторах , , :

| (, , )| = V. (14)

· Пояснение. Это следует из формул (3),(13), так как | (, , ) | = | × |=

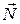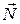=| |×| |× |cos j | = S × H = V; здесь S - площадьпараллелограммав основании параллелепипеда, j - угол между векторам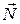и и ;

| |× | cos j| = H - высота параллелепипеда. ·

Правило. Имеет место следующая формула для смешанного произведения векторов (x 1; y 1; z 1), (x 2; y 2; z 2), (x 3; y 3; z 3 ):

(, , ) = (15)

· Пояснение. Выражение для (, , ) получается, если вектор (12) умножить скалярно на . Правая часть (12) есть сумма из 6 слагаемых. Рассмотрим одно из них: y 1 × z 2× 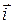. При скалярном умножении на вектор 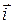заменяетсяна 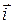× = x 3. Подобное рассуждение, примененное ко всем слагаемым в правой части (12), показывает, что формулу (15) можно получить заменой 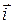, , в (12) на x 3, y 3, z 3 . ·

Применения смешанного произведения в геометрии.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)