Предел функции

Определение предела функции

Определение 4.1. Пусть функция f(х) определена на некотором интервале (а,в). Число А называется пределом функции f(х) в точке х_о, т.е.

,

если " e > 0 $ d = d(e) > 0: "х Î (а, в), удовлетворяющих условию

çх - х_оç < d, х ¹ х_о 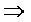(4.1)

çf(x) - Aç < e. (4.2)

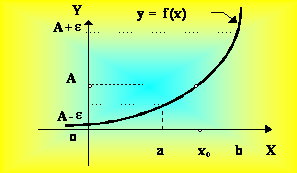Рис. 4.1.

Таким образом, число А называется пределом функции f(х) в точке х_о A = 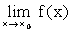, при х ® х_о тогда и только тогда, когда для любого (") e > 0 существует ($) такая дельта окрестность d = d (e) > 0 точки х_о:

"х Î (а, в): х Î O (х_о, d), х ¹х_о Þ f (x) Î O (A, e).

Поиск по сайту: