 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение плоскости пространстве
1-я ситуация. Известны одна точка M0 (x 0 ; y 0 ; z 0 ) плоскости Pи ненулевой вектор 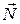 (A; B; C), перпендикулярный к этой плоскости (такой вектор называется нормальным вектором плоскости). для точек M(x; y; z) плоскости векторы
(A; B; C), перпендикулярный к этой плоскости (такой вектор называется нормальным вектором плоскости). для точек M(x; y; z) плоскости векторы 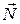 и
и 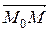 перпендикулярны, и их скалярное произведение равно нулю:
перпендикулярны, и их скалярное произведение равно нулю:
А (x - x 0) + B (y - y 0)+ C (z - z 0 )=0. (11)
Вводя постоянную D = - A x 0 – B y 0 – C z 0, получаем общее уравнение плоскости в пространстве:
A x + B y + C z + D = 0. (12)
Это – линейное уравнение для трех переменных, причем хотя бы один из коэффициентов A, B, C не равен нулю.
Для точек M (x; y; z), не лежащих на плоскости P, расстояние d до плоскости равно d = | A x + B y + C z + D | /  (ср. с формулой (5)).
(ср. с формулой (5)).
Замечание. В дальнейшем (в теме 8) используется уравнение плоскости с двумя угловыми коэффициентами. Пусть в уравнении (11) С ¹ 0, тогда уравнение плоскости приобретает вид z-z 0 =k 1 × (x-x 0 ) +k 2 × (y-y 0), где k 1 = - A / C, k 2 = - B / C.
Коэффициенты k 1 и k 2 имеют следующий геометрический смысл: k 1 (соответственно,
k 2 ) есть угловой коэффициент прямой, состоящей из точек данной плоскости с постоянным значением y = y 0 (соответственно, с постоянным значением x = x 0 ).
Свойства нормального вектора плоскости. (а) Если две плоскости параллельны, то их нормальные векторы коллинеарны (пропорциональны):
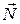 1 ´
1 ´ 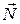 2 = 0. (б) Если две плоскости перпендикулярны, то их нормальные векторы
2 = 0. (б) Если две плоскости перпендикулярны, то их нормальные векторы
перпендикулярны: 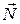 1×
1× 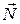 2 = 0. (в) Если a - угол между двумя плоскостями, то
2 = 0. (в) Если a - угол между двумя плоскостями, то
cos a = | 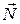 1 ×
1 × 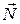 2 | / |
2 | / | 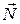 1 | × |
1 | × | 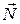 2|.
2|.
2-я ситуация. На плоскости P известны три точки M0(x 0; y 0; z 0),
M1(x 1; y 1; z 1), M2(x 2 ; y 2; z 2), не лежащие на одной прямой. Тогда уравнение
плоскости P записывается через определитель:
 =0. (13)
=0. (13)
· Пояснение. Вектор  является нормальным вектором плоскости P (см. применения векторного произведения в геометрии).
является нормальным вектором плоскости P (см. применения векторного произведения в геометрии).
Для точек M(x; y; z) векторы 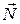 и
и 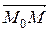 ортогональны, и их скалярное произведение равно нулю:
ортогональны, и их скалярное произведение равно нулю: 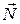 ×
× 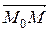 =
=  = 0. Теперь формула (13) следует из формулы (15)
= 0. Теперь формула (13) следует из формулы (15)
В частности, если известны три точки M0(a; 0; 0), M1(0; b; 0), m2(0; 0; c) плоскости, принадлежащие координатным осям O x,O y,O z, соответственно, то пишут
так называемое уравнение плоскости в отрезках: x / a + y / b + z / c = 1.
Поиск по сайту: