Способы задания функций

1. Если функция задана выражением при помощи формулы, то говорят, что она задана аналитически, Для этого используется некоторый запас изученных и специально обозначенных функций, алгебраические действия и предельный переход.

Например, .

Здесь - это совокупность действий, которые нужно выполнить в определенном порядке над значениями аргумента х, чтобы получить соответствующее значение функции y (или, то же самое, ).

Примеры:

1.

2. Функция Дирихле:

3.

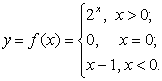
2. Функцию можно задавать таблично, т.е. для некоторых значений х указать соответствующие значения переменной y.

Данные такой таблицы могут быть получены как экспериментально, так и с помощью математических расчетов.

Примерами табличного задания функций могут быть: логарифмические таблицы, таблицы тригонометрических функций.

3. Аналитический и табличный способы задания функций страдают отсутствием наглядности.

(*)

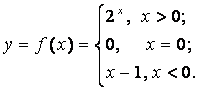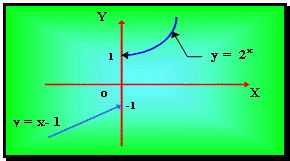Рис. 2.3.

Графический способ задания функции - это геометрическое место точек на плоскости с координатами .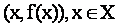

Поиск по сайту: