Понятие функции

Пусть заданы два множества Х и Y. Если каждому элементу х Х поставлен в соответствие один и только один элемент у У, обозначаемый f(х), и если каждый элемент у У при этом оказывается поставлен в соответствие хотя бы одному элементу х Х, то говорится, что на множестве Х задана однозначная функция у = f(х). Множество Х называется областью ее определения, а множество Y - множество ее значений. Элемент х Х называется аргументом или независимой переменной, а элементы у Y - значениями функции, или зависимой переменной..

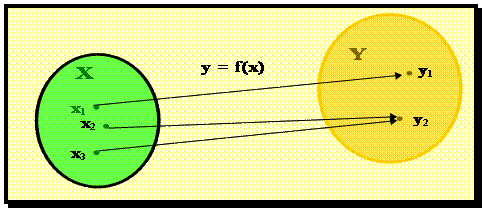
Рис. 2.1.

Элементы х и у рассматриваемых множеств могут иметь совершенно произвольную природу. Если значениями функции являются не числа, а другие элементы, часто вместо слова “функция” употребляют слово “отображение”.

Для того, чтобы задать функцию f, надо знать:

1. Х - область определения (существования);

2. Y - область значений;

3. Закон соответствия, по которому определяется элемент у Y, соответствующий х Х.

Поиск по сайту: