АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Понятие функции нескольких переменных

Читайте также:
  1. I. Понятие и значение охраны труда
  2. I. Понятие общества.
  3. II. ОСНОВНОЕ ПОНЯТИЕ ИНФОРМАТИКИ – ИНФОРМАЦИЯ
  4. II. Основные задачи и функции
  5. II. Понятие социального действования
  6. III. Предмет, метод и функции философии.
  7. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ
  8. А) ПЕРЕДАЧА НА РУССКОМ ЯЗЫКЕ ФУНКЦИИ АРТИКЛЯ
  9. А. Средняя квадратическая погрешность функции измеренных величин.
  10. Абстрактные классы и чистые виртуальные функции. Виртуальные деструкторы. Дружественные функции. Дружественные классы.
  11. Авторское право: понятие, объекты и субъекты
  12. Адаптивные функции

Рассмотрим вещественные функции, определенные на множестве n-мерного евклидового пространства Rn, значениями которого являются вещественные числа.

Эти функции обозначаются одним символом, например, или указывая аргумент – f(x), или и называются функциями многих переменных. Здесь переменные 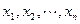называются независимыми переменными или аргументами. Совокупность рассматриваемых их значений - областью определения (областью существования).

Областью существования функции двух переменных (х и y), вообще говоря, представляет собой некоторое множество точек плоскости Oxy, т.е.

.

Аналогично для n=3.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)