Задача 2. Угол между двумя прямыми
Пусть даны уравнения двух прямых (не параллельных оси Oy) y=k 1 x+b 1и y = k 2 x+b 2, причем, k 1 = 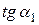 и k 2 = и k 2 = 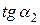 (k 1 < k 2). Тангенс угла j (k 1 < k 2). Тангенс угла j
    между положительными направлениями этих прямых (0 < j < p) можно определить из соотношения (рис. 3) между положительными направлениями этих прямых (0 < j < p) можно определить из соотношения (рис. 3)
  Рис. 3 Рис. 3  = = 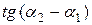 = = 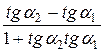 = =  . (5) . (5)

Замечание. Очевидно, второй угол, образованный прямыми, равен p -j.
Пример 4. Найти угол между положительными направлениями прямых y = 2 x + 51 и y = 3 x - 19.
Решение. Здесь k 1 = 2, k 2 = 3, k 1 < k 2. По формуле (5)  = = 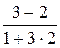 = = 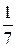 ; искомый угол j = ; искомый угол j = 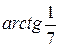 . ■ . ■
Пример 5. Найти углы между прямыми y =  x - 6 и x = 2. x - 6 и x = 2.
Решение. Здесь пользоваться формулой (5) невозможно, т.к. прямая x = 2 не имеет углового коэффициента. Так как угол наклона первой прямой к оси Ox может быть найден из определения углового коэффициента:  = =  и j= 60°, то угол между положительным направлением этой прямой и положительной полуосью Oy равен 90°-60°=30°. Следовательно, и один из искомых углов равен 30° (другой угол равен 180°-30°=150°). ■ и j= 60°, то угол между положительным направлением этой прямой и положительной полуосью Oy равен 90°-60°=30°. Следовательно, и один из искомых углов равен 30° (другой угол равен 180°-30°=150°). ■
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | Поиск по сайту:
|

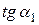 и k 2 =
и k 2 = 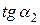 (k 1 < k 2). Тангенс угла j
(k 1 < k 2). Тангенс угла j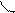

 между положительными направлениями этих прямых (0 < j < p) можно определить из соотношения (рис. 3)
между положительными направлениями этих прямых (0 < j < p) можно определить из соотношения (рис. 3)
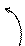
 Рис. 3
Рис. 3  =
= 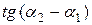 =
= 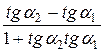 =
=  . (5)
. (5)

 =
= 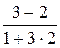 =
= 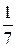 ; искомый угол j =
; искомый угол j = 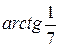 . ■
. ■ x - 6 и x = 2.
x - 6 и x = 2. =
=  и j= 60°, то угол между положительным направлением этой прямой и положительной полуосью Oy равен 90°-60°=30°. Следовательно, и один из искомых углов равен 30° (другой угол равен 180°-30°=150°). ■
и j= 60°, то угол между положительным направлением этой прямой и положительной полуосью Oy равен 90°-60°=30°. Следовательно, и один из искомых углов равен 30° (другой угол равен 180°-30°=150°). ■