Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами

Антология

Часть 1

Под редакцией С. П. Баньковской

Данное издание выпущено в рамках программы Центрально-Европейского Университета «Books for Civil Society» при поддержке Центра по развитию издательской деятельности (OS1 — Budapest)и Института «Открытое общество» (Фонд Сороса) — Россия

Теоретическая социология: Антология: В 2 ч. / Пер. с англ., фр., нем., ит. Сост. и общ. ред. С. П. Баньковской. — М.: Книж­ный дом «Университет», 2002. — Ч. 1. — 424 с.

ISBN 5-8013-0151-8 (ч. 1)
ISBN 5-8013-0046-5

Цель настоящего издания — представить развитие социальной теоре­тической мысли от классиков до современных теоретиков. Поскольку соб­ственно научное теоретизирование о социальном связано с осмыслением современности, то хронологически классический период относится к кон­цу XIX - началу XX века; подбор материалов начинается именно с этого периода.

Особенностью данного издания можно считать то, что в нем представ­лены не только уже хорошо известные имена и работы, но и ранее не пере­водившиеся на русский язык авторы или работы известных теоретиков,

В данной антологии развитие представлений о социальном дано в тео­ретическом контексте, не ограниченном строгими дисциплинарными рам­ками; в собрание включены материалы из области социальной философии, антропологии, политической науки, социальной психологии и собственно социологии.

Издание предназначено для студентов, аспирантов, преподавателей, ученых, специализирующихся в социальных науках, для всех интересую­щихся проблемами современного общества.

УДК 316.1(075.8) ББК 60.5я73

© Баньковская С. П., составление, перевод. 2002
© Гофман А. Б., Зотов А. А., Ковалев А Л

© Малинкин А. П., Руткевич Е. Д.

© Филиппов А. Ф., перевод, 2002

Матрицы и определители

1. 1 Матрицы. Понятия.

Прямоугольной матрицей размера m x n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

A = (4.1)

или сокращенно в виде A = (a_ij) (i = 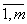; j = 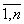). Числа a_ij, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (a_ij) и B = (b_ij) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_ij = b_ij.

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m x n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

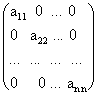Если все элементы a_ii диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

E = .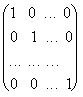

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Поиск по сайту: