АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение систем линейных уравнений с помощью определителей

Читайте также:
  1. A) к любой экономической системе
  2. A) прогрессивная система налогообложения.
  3. C) Систематическими
  4. CASE-технология создания информационных систем
  5. I СИСТЕМА, ИСТОЧНИКИ, ИСТОРИЧЕСКАЯ ТРАДИЦИЯ РИМСКОГО ПРАВА
  6. I. Основні риси політичної системи України
  7. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  8. I. Решение логических задач средствами алгебры логики
  9. I. Суспільство як соціальна система.
  10. I. Формирование системы военной психологии в России.
  11. I.2. Система римского права
  12. II. Решение логических задач табличным способом

Применяется при условии m = n.

Составим определитель из коэффициентов при неизвестных системы линейных уравнений, у которой n уравнений и n неизвестных. Такой определитель называют основным определителем системы.

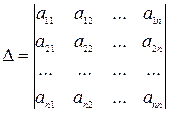
Составим вспомогательные определители для данной системы следующим образом:

Δ1 – определитель, который получается из основного определителя заменой его первого столбца столбцом свободных членов системы.

...................

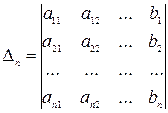
Неизвестные данной системы можно найти по формуле Крамера:

; ; …; .

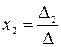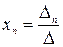1) Если основной определитель системы отличен от нуля, то такая система уравнений имеет единственное решение – она совместна и определенна, и это решения находят по формуле Крамера;

2) Если основной определитель системы равен нулю, то система уравнений может быть совместной неопределенной (∞ решений) или несовместной (не имеет решений):

а) Если основной определитель системы равен нулю и все вспомогательные определители равны нулю, то система уравнений имеет ∞ решений;


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)