 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Скалярное произведение
|
Читайте также: |
Скалярное (т.е. числовое) произведение 
двух геометрических векторов
и 
определяетсякакпроизведение длин этих векторов и косинуса угла между ними:
= | | × | |×cos j, (3)
где | | и | | - длины (модули, абсолютные величины) векторов, а j - угол между векторами. Скалярное произведение можно выразить через (числовую) проекцию Пр 
вектора на вектор :
= | | × Пр . (4)
В частности, длина вектора связана со скалярным произведением:
= | | 2 . (5)
Механическое истолкование скалярного произведения: - это работа, которую производит источник силы при перемещении предмета на вектор .
(Например, источники силы трения производят отрицательную работу и, значит,
приобретают энергию - нагреваются; в этом примере cos j < 0.)
Свойства скалярного произведения: 1) = 
; 2) ×(k ) =
= k (k – число); 3) × ( + 
) = + × .
Свойства 2) и 3) получаются из формулы (4) и соответствующих свойств проекций. Они означают, что при скалярном умножении векторов скобки раскрываются, как при умножении чисел. Например, (2 -3 ) × = 2 × – 3 × .
Из определения (3) легко вывести «таблицу» скалярного умножения ортов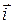 
, 
, 
:
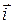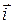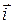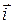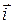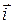× = × = × = 1, × = × = × = × = × = × = 0.
Разлагая векторы и по ортам и используя «таблицу» скалярного умножения ортов, получаем.
Правило. Имеет место алгебраическая формула для скалярного произведения
векторов (x 1; y 1; z 1)и (x 2; y 2 ; z 2):
× = x 1× x 2+ y 1× y 2 + z 1× z 2. (6)
Примененияскалярного произведения в геометрии.
1) Длина вектора (x; y; z):
ï ï = (x 2+ y 2 + z 2) 1 / 2 (7)
(это - следствие формул (5) и (6)).
2)Расстояние между двумя точками A1 иA2:
ï 
ï =((x 2- x 1)2+(y 2- y 1)2+(z 2- z 1)2)1/2. (8)
3)Косинус угла между двумя векторами и :
cos j = × / ê ê× ê ê. (9)
4)Если два (ненулевых) вектора и перпендикулярны (ортогональны),то
× = 0. И наоборот. (Слово orthogonal переводится как «прямоугольный»).
Замечание. В задачах, в которых фигурируют только точки и векторы на координатной плоскости O xy, координата z (равная нулю) не пишется. В этой ситуации применяют формулы, аналогичные (6)-(9). Например, расстояние между двумя точками теперь вычисляется по формуле
| A1A2 |= ï 
ï =((x 2 - x 1)2 + (y 2- y 1)2) 1/ 2. (10)
Поиск по сайту: