Рассмотрим три способа составления уравнения прямой в зависимости от исходных данных

1-я ситуация. Известны одна точка M₀(x ₀ ; y ₀) на прямой и угловой коэффициент k прямой L.Тогда уравнение прямой пишется так:

y – y ₀= k × (x – x ₀).

· Пояснение. В формуле (6) параметр k известен, а параметр b не известен. Чтобы исключить его из (6), учтем, что точка M₀ лежит на прямой: y ₀= k x ₀+ b. Вычтем это уравнение из (6). Получим: y - y ₀= k ×(x - x ₀). ·

2-я ситуация. Известны одна точка M₀ (x ₀ ; y ₀ ) на прямой L и ненулевой вектор (l; m),параллельный прямой (такой вектор называется направляющим). В этой ситуации пишут так называемое каноническое уравнение прямой на плоскости:

(8)

· Пояснение. Для точек M (x; y) на прямой L вектор 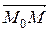параллелен вектору ,и значит, пропорционален ему: 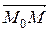= t × . Множитель (переменная величина) t называется параметром на прямой. Запишем это в координатах: x - x ₀= t × l,

y - y ₀ = t × m. (это – т.наз. параметрические уравнения прямой на плоскости.)Исключая отсюда t, получим (8). Может оказаться, что один из знаменателей в (8) равен нулю, например, l = 0. Запись (x – x ₀)/ 0 =(y - y ₀) / m есть условность(ее нельзя понимать буквально). Чтобы «расшифровать» ее, возвращаемся к параметрическим уравнениям прямой и получаем корректное уравнение данной прямой: x - x ₀ = 0.·

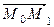3-я ситуация. Известны две точки M₀(x ₀ ; y ₀) и M₁(x ₁ ; y ₁ ) на прямой L. Тогда уравнение прямой также пишется в каноническом виде, причем роль направляющего вектора (l; m) играет вектор (x ₁– x ₀ ; y ₁ - y ₀):

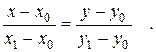(9)

В частности, если известны две точки M₀ (a; 0) и M₁(0; b) прямой, принадлежащие координатным осям O x иO y, соответственно, то пишут так называемое уравнение прямой в отрезках: x a + y b = 1.

Поиск по сайту: