Размерность квадратной матрицы называется ее порядком

Если определитель квадратной матрицы ≠ 0, то такая матрица – невырожденная (неособенная);

Если определитель квадратной матрицы = 0, то такая матрица – вырожденная (особенная).

Квадратная матрица вида

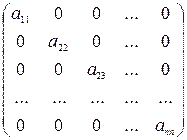
где а ₁₁, а ₂₂, …, а_nn – элементы, распределенные по главной диагонали, называется диагональной матрицей.

Диагональная матрица, все элементы которой по главной диагонали равны 1, называется единичной матрицей (E _n).

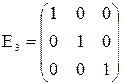
Любое число можно считать матрицей первого порядка.

Если у матрицы переставить местами столбцы со строками, то такая операция называется транспонированием матрицы.

А^т – транспонированная матрица.

|А| = |А^т| (если А – квадратная)

(А^т)^т = А

Квадратная матрица называется симметрической, если А = А^т, т.е. a_ij = a_ji для любых i и j.

Поиск по сайту: