Возведение квадратной матрицы в целую степень

Операция перемножения матриц дает возможность путем повторного умножения реализовать операцию возведения квадратной матрицы в целую степень. Это, в свою очередь, позволяет вычислять матричные степенные ряды, через которые выражаются матричные функции матричного аргумента. Рассмотрим алгоритм возведения квадратной матрицы A, содержащей n строк и n столбцов в степень m. Результирующую матрицу будем именовать B.

B = A^m = E x A x A x...x A,

где E – единичная матрица. Операция умножения выполняется m раз.

Блок-схема этого алгоритма представлена на рис. 28.20. Она представлена на двух уровнях детализации. На первом уровне (изображение слева) основные блоки представлены укрупненно. На изображении справа первый и последний блоки детализированы до основных алгоритмических конструкций. Блок умножения матрицы на матрицу не детализирован, т.к. он рассмотрен в предыдущем подразделе и предполагается, что в данном алгоритме он реализован как вызов вспомогательного алгоритма.

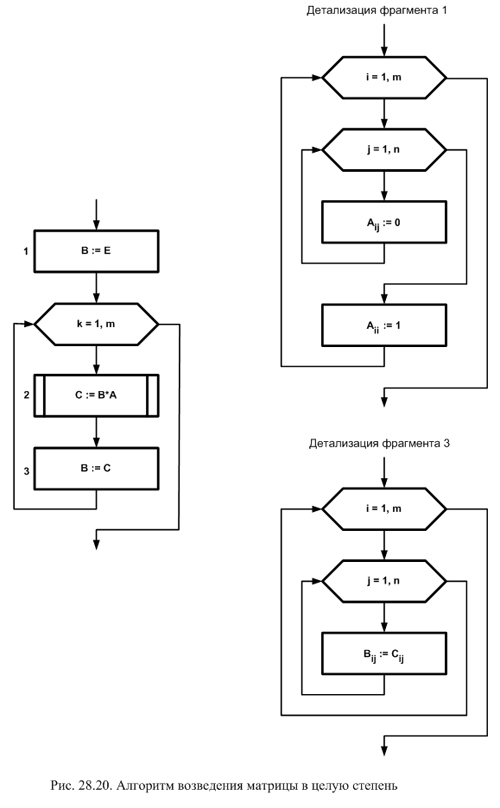
В основе алгоритма лежит цикл повторного умножения (по переменной k), который выполняется m раз. До начала цикла в выходной матрице B формируется единичная матрица. В теле основного цикла вызовом вспомогательного алгоритма выполняется умножение матрицы B на возводимую матрицу A, результатом является матрица C. Второй фрагмент тела цикла заключается в передаче данных от матрицы С матрице B. Детализации первого и третьего блока просты и не требуют особых пояснений.

Поиск по сайту: