Решение уравнений итерационными методами

Циклы с пред- и послеусловием используются при решении уравнений вида F(x) = 0 итерационными методами. Левая часть уравнения F(x) предполагается такой, что аналитическое решение получить невозможно. Численные итерационные методы позволяют получить решение методом последовательных приближений – итераций, на каждой из которых находится новое, уточненное решение. Задав нулевое приближение корня x₀, по некоторой итерационной формуле вычисляется приближение x₁. По нему, используя ту же итерационную формулу вычисляется x₂, затем – x₃ и так далее. Итерации останавливаются, когда разница между двумя последними найденными значениями станет по абсолютной величине меньше заданной погрешности ε: | x_k – x_k-1 | < ε. Последнее значение x_k принимается за искомое решение.

Метод простых итераций требует преобразования уравнения F(x) = 0 к виду x = f(x). Из этого вида следует итерационная формула:

x_k = f(x_k-1),

где k = 1, 2, 3, … - индекс итерации. Метод простых итераций обеспечивает сходимость вычислений к корню, если на интервале итераций выполняется условие .

Блок-схема метода простых итераций на основе цикла с послеусловием приведена на рис. 28.3. Итерационная формула разбивается на три части, сначала на итерации по входящему в нее значению x вычисляется новое приближение корня xk, затем - разность dx = xk – x, а далее выполняется переприсвоение x = xk для выполнения новой итерации. Разность dx используется для проверки условия повторения итераций.

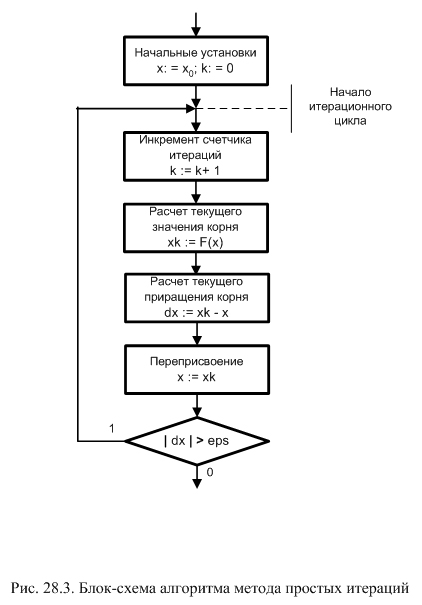
В реальной практике для решения нелинейных уравнений чаще всего используется метод Ньютона. Он использует следующую итерационную формулу:

,

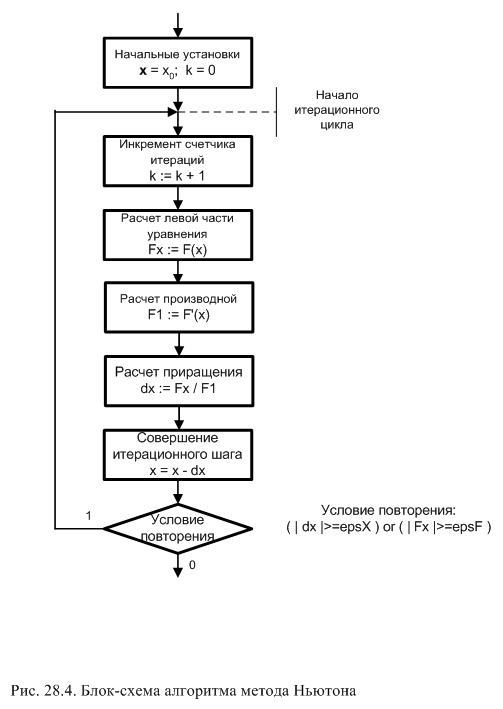
где F'(x) - производная левой части уравнения. Метод обеспечивает быструю сходимость итераций, если на их интервале первая и вторая производные левой части уравнения не изменяют знаки. Его блок-схема представлена на рис. 28.4. Алгоритм реализован на основе цикла с послеусловием, хотя может быть использован и цикл с предусловием. Тело цикла реализует итерационную формулу и не требует пояснений. Логическое выражение при завершении цикла состоит из двух условий, соединенных по ИЛИ. Цикл повторяется, если приращение неизвестной больше или равно погрешности ε_x, или левая часть уравнения по абсолютной величине больше или равна погрешности ε_f. Использование двух погрешностей позволяет, кроме нахождения корня с заданной погрешностью, добиться и малой невязки левой части уравнения с нулем.

Поиск по сайту: