Алгоритмы упорядочивания элементов в массивах

Алгоритмы упорядочивание элементов одномерных массивов по возрастанию или убыванию их величины (сортировки) являются одними из важнейших в программировании. Существует достаточно много различных алгоритмов сортировки; здесь рассматривается только два из них.

Первый алгоритм достаточно прост по сути; он строится на основе изложенного в 28.7. Рассмотрим его на примере упорядочивания по возрастанию n элементов одномерного массива X. Он основан на следующих действиях.

Сначала находится минимальный элемент массива в ряду от первого до последнего, n -ного. Этот элемент Xm c индексом im обменивается местами с первым. Затем находится новый минимальный элемент в ряду от второго до последнего. Он обменивается местами со вторым. И так далее. Цикл поиска и обмена местами повторяется до предпоследнего элемента, т.е. n-1 раз. Блок схема этого алгоритма представлена на рис. 28.15.

Если найденный минимальный элемент совпадает с начальным элементом поиска, то его не нужно обменивать местами. Но для некоторого упрощения в блок-схеме исключена проверка этого случая и сохранен обмен элемента с самим собой. Обмен элементов местами производится через вспомогательную переменную tmp.

Проанализируем работу этого алгоритма на примере массива из четырех элементов:

При первом исполнении основного цикла будет найден минимальный четвертый элемент и обменен местами с первым:

При втором прохождении будет найден минимальный третий элемент и обменен местами со вторым:

И наконец, при последнем прохождении цикла будет найден минимальный четвертый элемент, обменен местами с третьим и все элементы окажутся упорядочены.

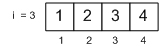
Более эффективным является другой алгоритм сортировки, называемый пузырьковым. Его блок-схема приведена на рис. 28.16. Он является более компактным, чем предыдущий. Проанализируем его работу на таком же примере. Для наглядности изобразим вертикальное расположение ячеек массива при возрастании номера сверху вниз.

Исходное состояние элементов массива следующее:

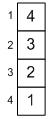
При первом исполнение тела внешнего цикла внутренний цикл будет исполняться трижды. При этом сначала обменяются местами третий и четвертый элементы, затем – второй и третий и, наконец, первый и второй. В результате этих обменов элемент массива, равный 1, как пузырек воздуха, всплывает вверх:

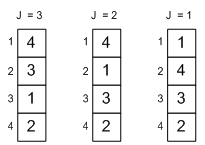
При втором исполнение тела внешнего цикла внутренний цикл будет исполняться два раза. Сначала обменяются местами третий и четвертый элементы, а затем – второй и третий.

При последнем исполнении тела внешнего цикла внутренний цикл исполняется один раз и в нем переставляются местами третий и четвертый элементы;

Сортировка завершена.

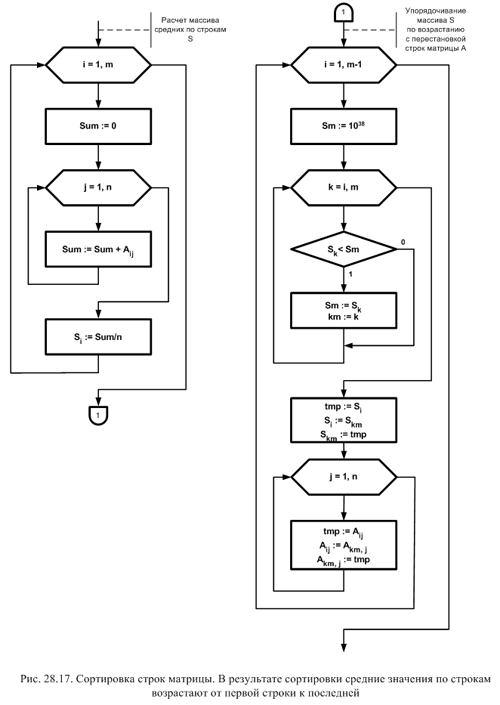
Алгоритмы упорядочивания матриц оказываются более сложными. Приведем в качестве при-мера алгоритм перестановки строк матрицы, в результате которой средние значения элементов по строкам возрастают от первой строки к последней. Он представлен на рис. 28.17.

Матрица A имеет m строк и n столбцов. Сначала в цикле по индексу строки i рассчитываются средние значения по строкам; их значения записываются в массив S. Затем производится сортировка элементов массива S по возрастанию первым из описанных выше методом. При перестановке элементов массива S одновременно переставляются связанные с ними строки матрицы. После окончания сортировки массива S все строки матрицы A оказываются упорядочены нужным образом.

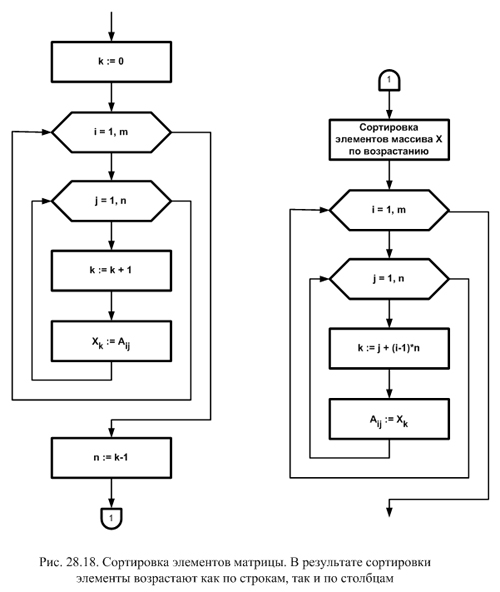
Второй алгоритм, представленный на рис. 28.18 упорядочивает элементы матрицы A из m строк и n столбцов так, чтобы они возрастали как по строкам, так и по столбцам. Для этого используется вспомогательный одномерный массив X. Сначала элементы матрицы A по строкам переписываются в одномерный массив X, затем упорядочиваются там пузырьковым методом, а затем переписываются обратно в той же последовательности по строкам. При переписывании данных из двумерного массива в одномерный и обратно использованы два разных способа установления соответствия между индексами двумерного и одномерного массивов. В первом случае индекс одномерного массива формируется как счетчик, который сначала обнуляется, а в теле цикла перезаписи увеличивается на единицу. Во втором случае используется соответствие между индексами i (строки) и j (столбца) матрицы и индексом k одномерного массива:

k = j+(i-1)*n

Оба этих способа эквивалентны. На блок-схеме фрагмент упорядочивания одномерного массива не детализирован, т.к. он совпадает с приведенным на рис. 28.16.

Для исполнения этой задачи может быть предложен более оптимальный алгоритм, не использующий одномерный массив и представляющий собой двумерный вариант алгоритма на рис. 2.15. Однако приведенный вариант с одномерным массивом полезен тем, что показывает приемы перезаписи элементов из двумерного массива в одномерный и обратно, что иногда требуется при разработке алгоритмов.

Поиск по сайту: