Алгоритмы обхода дерева

Существуют три алгоритма обхода деревьев, которые естественно следуют из самой структуры дерева.

1. Обход слева направо: Left-Root-Right (сначала посещаем левое поддерево, затем – корень и, наконец, правое поддерево).

2. Обход сверху вниз: Root-Left-Right (посещаем корень до поддеревьев).

3. Обход снизу вверх: Left-Right-Root (посещаем корень после поддеревьев).

Интересно проследить результаты этих трех обходов на примере записи формулы в виде дерева, так как они и позволяют получить различные формы записи арифметических выражений.

Пусть для операндов А и В выполня­ется операция сложения. Привычная форма записи в виде А + В называется ин­фиксной. Форма записи, в которой знак операции следует перед операндами + АВ, называется префиксной, если же операция записывается после операндов АВ + – постфиксной.

Рассмотрим небольшой пример, пусть задано выражение А + В * С. Так как умножение имеет более высокий приоритет, то данное выражение можно переписать в виде А +(В * С). Для записи выражения в постфиксной форме сначала преобразуем ту часть выражения, которая вычисляется первой, в результате получим: А +(ВС *).

Теперь запишем в постфиксной форме операцию сложения между операндами А и (ВС *): АВС *+.

Таким образом, выражение А + В * С в постфиксном виде АВС *+, префиксная форма записи будет иметь вид +* АВС.

Рассмотрим различные обходы дерева на примере формулы: ((a + b / c)*(d – e * f)). Дерево формируется по принципу:

– в корне размещаем операцию, которая выполнится последней;

– далее узлы-операции, операнды – листья дерева.

Обход 1 (Left-Root-Right) дает обычную инфиксную запись выражения (без скобок):

a + b / c * d – e * f.

Обход 2 (Root-Left-Right) – префиксную запись выражения (без скобок):

* + a / b c – d * e f.

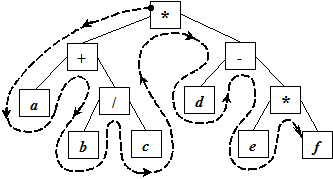
Обход 3 (Left-Right-Root) – постфиксную запись выражения:

a b c / + d e f * – *.

Поиск по сайту: