 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Итерационные алгоритмы размещения
Эти алгоритмы предполагают заданным некоторое начальное размещение, которое может быть получено некоторым конструктивным алгоритмом размещения. Исследуются некоторое множество возможных вариантов размещения близких в некотором смысле к начальному и находящие размещение с меньшим значением целевой функции Lсуммарное. Найденное размещение принимается за исходное и процесс повторяется. Алгоритм заканчивает работу если в окрестности полученного размещения отсутствуют варианты с меньшими значениями целевой функции.
Различают 2 группы итерационных алгоритмов:
1. алгоритмы парных перестановок
2. алгоритмы групповых перестановок
Алгоритм парных перестановок.
Суть: Последовательное целенаправленное улучшение произвольного начального размещения модулей на плате по выбранному критерию путем парных перестановок. С этой целью на каждой итерации алгоритм осуществляет вычисление приращенной суммарной длины всех связей для всевозможных парных перестановок модулей. Из всего множества перестановок дающих отрицательное приращение выбирается подмножество которое удовлетворяет следующим требованиям:
1. выбранное подмножество перестановок позволяет max уменьшить суммарную длину всех связей.
2. подмножество образует лишь независимые перестановки в которых модули несвязанны с модулями других переставляющихся пар.
Далее осуществляется перестановки выделенных таким образом пар модулей и переход к следующей итерации.
Описанный итерационный процесс сходится к локальнооптимальному размещению модулей на плате. Выведем формулы для суммарной длины L всех связей и ее приращение 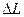 при перемещение модулей.
при перемещение модулей.
Пусть имеется плоское или объемное плато с узлами предназначенными для установки модулей, задана матрица расстояний D=||dij||n*n где dij определяется в обычной или ортогональной метриках.
Даны некоторые совокупности модулей подлежащих размещению и матрица C=||cij||n*m числа связей этих модулей между собой.
Пусть на некоторой итерации имеется следующее размещение модулей на плате:
… 1 2 3 … e … n
 мод t1 t2 t3 … te … tn
мод t1 t2 t3 … te … tn
te- номер модуля оказавшегося размещенным в узле платы.
Поставим в соответствие этому варианту размещения матрицу связей R=||rij||n*n. Элемент rij=числу связей между модулями ti и tj находится на данной итерации в узлах i и j соответственно.
Так как расстояние между узлами i и k равно dik то суммарная длина связей между модулями ti и tk:
lik=rik*dik (1)
отсюда суммарная длина связей ti модуля расположенного в i-ом узле связаны со всеми модульными схемами равна:
 (2)
(2)
Для суммарной длины всех связей при данном варианте получаем формулу:
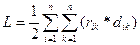 (3)
(3)
Примечание: пусть i=k=  тогда
тогда 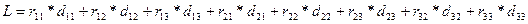
Найдем формулу для приращения суммарной длины всех связей при перестановке мудулей ti и tj расположенных в узлах i и j соответственно.
Для суммарной длины связей ti и tj со всеми остальными модулями имеем:
 (4)
(4)
Замечание: пусть n=4 i=2 j=3

Найдем формулу для приращения суммарной длины всех связей при перестановке модулей ti и tj расположенных в узлах i и j соответственно. Для суммарной длины связей ti и tj модулей со всеми оставшимися модулями имеем:
 (5)
(5)
Заметим, что за n-ое число перестановок модулей ti и tj соответствует перестановке строк и столбцов с номером i и j в матрице R. Вычитая из (5) выражение (4) определим приращение суммарной длины всех связей после перестановки модулей с номером ti и tj.
 i,j=
i,j=  (6)
(6)
Введем в рассмотрение матрицу P=R x D,
 .
.
Полусумма диагональных элементов матрицы P (полуслед) равна суммарной длине всех связей, определяемой формулой (3). С помощью элементов матрицы P могут быть легко вычислены элементы ∆Lij матрицы приращений для всех парных перестановок. С учетом симметричности матрицы D выражение (6) преобразуется к виду:
 ;
;
где 
Вычисляя по выражениям (8) и (9) элементы матрицы приращений ∆L можно выбрать подмножество перестановок, удовлетворяющих вышеперечисленным требованиям.
Пример.
Пусть начальное размещение связано с системой модулей на плате с 6-ю узлами имеет вид, представленный на рисунке:

Во втором узле размещен разъем, который запрещено переносить на другую позицию. Если расстояния dij между узлами i и j определены в ортогональной метрике, то матрица D будет иметь вид:
| p1 | p2 | p3 | p4 | p5 | p6 | |||
| p1 | ||||||||
| p2 | ||||||||
| D | = | p3 | ||||||
| p4 | ||||||||
| p5 | ||||||||
| p6 |
| e1 | e2 | e3 | e4 | e5 | e6 | |||
| e1 | ||||||||
| e2 | ||||||||
| R | = | e3 | ||||||
| e4 | ||||||||
| e5 | ||||||||
| e6 |
Составим соответствующую начальному размещению матрицу P=R x D. Элемент p11 определяется из выражения: p11=r11d11+r12d21+r13d31+r14d41+r15d51+ +r16d61= 0+1∙1+0+1∙1+0+0=2 и т. д. и т. п.
| P | = | |||||||
Суммарная длина всех связей в начальном размещении равна полуследу матрицы P:  .
.
Вычислим далее последовательно матрицы γ, γ*, Q и ∆L:
| -6 | -3 | -4 | ||||||||
| γ | = | || pij–pii || | = | -5 | -5 | -12 | -7 | |||
| -2 | -10 | -6 | -8 | -4 | ||||||
| -4 | -10 | -6 | ||||||||
| -1 | -4 | -3 |
| -6 | -2 | -1 | ||||||||||
| -5 | -10 | -4 | ||||||||||
| γ* | = | || pij–pii || | = | γT | = | -6 | -10 | |||||
| -3 | -5 | -4 | ||||||||||
| -4 | -12 | -8 | -3 | |||||||||
| -7 | -4 | -6 |
| -6 | -2 | |||||||||
| -20 | -8 | |||||||||
| Q | = | γ+γ* | = | -11 | -22 | -4 | ||||
| симметр. | -2 | -8 | ||||||||
| -9 | ||||||||||
| –– | –– | –– | –– | |||||
| –– | –– | –– | –– | |||||
| ∆L | = | -11 | -2 | |||||
| симметр. | ||||||||
| -7 | ||||||||
∆Lij=2rijdij (>0) +qij (>, <, =0)
В матрице ∆L прочерком указаны элементы, которые заведомо являются положительными в силу положительности соответствующих элементов матрицы Q, а также элементы отвечающие недопустимому переразмещению модуля 2 (разъема). Из рассмотрения матрицы ∆L видно, что к уменьшению суммарной длины всех связей приводят взаимные перестановки пар модулей, расположенных в начальном размещении в следующих узлах: 3 и 4 (∆L =-11), 3 и 6 (∆L =-2), 5 и 6 (∆L =-7).
Примечание. Пары модулей {ei и ej} и {ek и eq} являются независимыми если элементы матрицы связей R равны нулю. Для нашего примера допустимой является лишь одна перестановка (пара 3 и 4), обеспечивающая | ∆Lmax |=11.
Производим перестановку элементов e3 и e4 (см. рис.):

Для нового варианта размещения находим матрицы R и P. С этой целью необходимо в матрице R, соответствующей начальному варианту размещения поменять местами элементы 3-го и 4-го столбцов и 3-ей и 4-ей строк. Матрица P получается умножением новой матрицы R на старую D.
| P | = | |||||||
Суммарная длина всех связей нового варианта
 .
.
Выполним следующую итерацию.
| -2 | -2 | |||||||
| -4 | ||||||||
| γ | = | -4 | -2 | |||||
| -7 | ||||||||
| -4 | ||||||||
| -1 |
| -8 | ||||||||
| Q | = | |||||||
| -11 | ||||||||
| –– | –– | –– | –– | –– | ||||
| –– | –– | –– | –– | |||||
| ∆L | = | –– | –– | –– | ||||
| –– | ||||||||
| –– | ||||||||
Матрицы ∆L не имеет ни одного отрицательного элемента, поэтому процесс улучшения начального размещения закончен. Т. о., размещение, изображенное на последнем рисунке соответствует локальному оптимуму.
Блок-схема алгоритма парных перестановок.

Поиск по сайту: