Последовательные алгоритмы размещения по связности

Сущность этого многошагового алгоритма сводится к последовательному размещению очередного модуля (элемента) в определенный узел платы. Предполагается что часть модулей (или хотя бы один) заранее размещены на монтажной плоскости. В качестве таких модулей могут быть выбраны либо контакты разъема, либо модули, фиксированные в определенных позициях в соответствии с директивными указаниями разработчика. При выборе очередного модуля оптимизируется целевая функция, учитывающая связи этого модуля с множеством ранее размещенных и неразмещенных модулей. В качестве такой функции, например, может быть выбрана следующая:

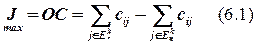
где c_ij – элемент матрицы смежности ВНГ; – соответственно множества размещенных и неразмещенных на k –м шаге алгоритма модулей.

Задача размещения при этом сводится к максимизации оценки (6.1) по всем модулям, принадлежащим множеству .

Далее для выбранного модуля находится наиболее приемлемая позиция на плате. Для выбора такой позиции используется критерий минимальности длины связей размещаемого модуля с уже размещенными модулями. При этом, очевидно, нет необходимости рассматривать все незанятые на этом шаге позиции, а достаточно оценить лишь множество позиций, соседних с занятыми. При этом позиция p_i, в которую необходимо поместить i –й модуль, определяется из условия минимизации следующего выражения:

где c_ij – элемент матрицы смежности ВНГ; R^k –множество позиций, соседних с занятыми, на k –м шаге.

Рассмотрим работу последовательного алгоритма размещения по связности на примере (рис. 6.1).

Рис. 6.1.

Пусть элемент e₂ директивно помещается в 6-ю позицию, элемент e₃ директивно помещается в 9-ю позицию.

Чтобы выбрать очередной размещаемый модуль, необходимо в соответствии с (6.1) найти модуль с максимальной оценкой J.

П. 1.

Вычисляем оценки по связности для каждого неразмещенного модуля:

Элементы e₁ и e₅ имеют максимальную оценку, равную +1. Для дальнейшего анализа выбираем элемент e₁ (с меньшим порядковым номером).

П. 1.1.

Модуль e₁ в соответствии с (6.2) размещаем во 2-ю позицию (с меньшим порядковым номером) (см. ниже).

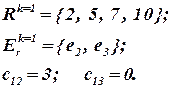
Определим F, предполагая, что модуль e₁ размещен

Окончательно размещаем e₁ во 2-ю позицию (с меньшим порядковым номером) и корректируем массив соседних позиций.

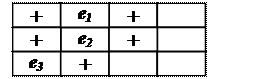
П. 2.

Определим следующий модуль для размещения.

Модуль e₅ имеет максимальную оценку, равную +1. в соответствии с (6.2) он помещается в 5-ю позицию.

И т. д. и т. п.

Окончательный вариант размещения представлен на рис. 6.2.

Рис. 6.2.

Укрупненная схема последовательного алгоритма размещения приведена на рисунке 6.3.

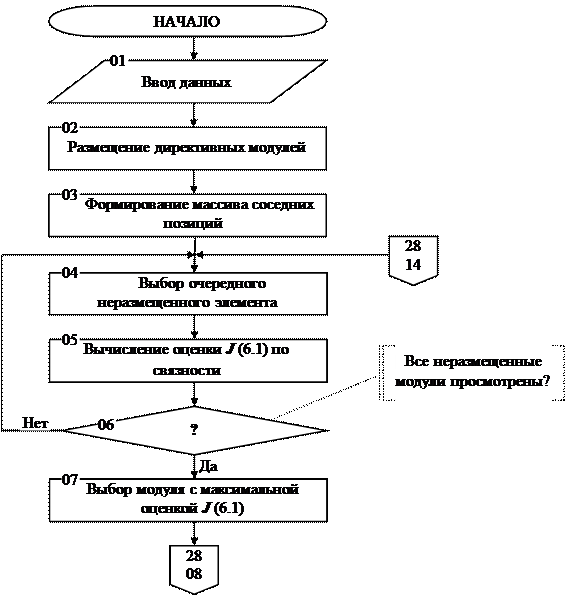
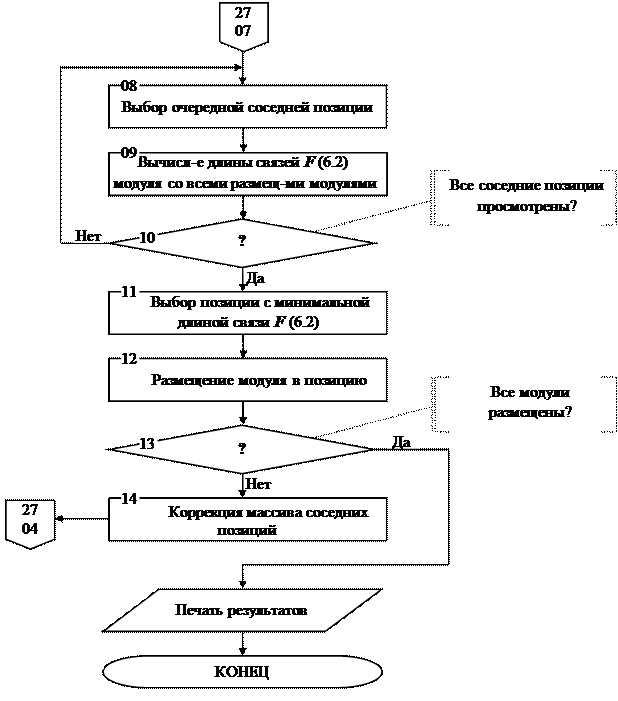
Рис. 6.3. Схема последовательного алгоритма размещения.

Приведем краткий перечень идентификаторов для реализации последовательного алгоритма размещения.

L – число элементов;

D – число директивных элементов;

M – число позиций по горизонтали;

N – число позиций по вертикали;

E(I) – массив директивных элементов;

P(I) – массив директивных позиций;

POS(LI) – номер позиции, в которую размещается элемент с номером LI;

Z(I) – массив соседних позиций;

SP1 – список элементов, связанных с данным элементом;

SP2 – список количества связей между элементами;

RSP – список, устанавливающий связность SP1 и SP2.

Приведем фрагмент развернутой блок схемы алгоритма позволяющей определить элемент или максимальную оценку.

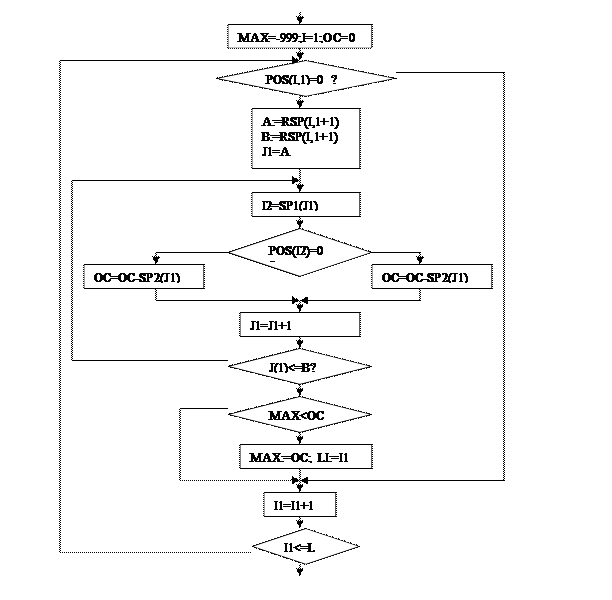
Учтем, что списки имеют вид SP1=(2,4,9), SP2=(1,1), RSP(1)=0, RSP(1+1)=1, RSP(2)=3 от E(1) переходим к E(4).

При выборе позиции элемента ei часто используется не модель ВНГ а модель ГГ в этом случае при определении позиции можно учесть взаимное расположение элемента в цепи, а также использовать в качестве оценки для позиции критерий минимизации многоугольника охватывающего элементы цепи.

Поиск по сайту: