АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Математическая постановка задачи компоновки с использованием модели ВНГ

Читайте также:
  1. Can-Am-2015: новые модели квадроциклов Outlander L и возвращение Outlander 800R Xmr
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Ситуационные задачи и тестовые задания.
  4. II. Основные задачи и функции
  5. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  6. II. Цель и задачи государственной политики в области развития инновационной системы
  7. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  8. III.3. Естественнонаучная и математическая мысль эпохи Средневековья
  9. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  10. YIII.5.2.Аналогия и моделирование
  11. Авторегрессионные модели временных рядов
  12. Алгоритмизация модели и её машинная реализация

Критерий оптимизации – число межблочных связей. ВНГ будем представлять в виде матрицы C.

Введем в рассмотрение матрицу решений ξ, которая определяет вариант компоновки элементов схемы в блоки.

На элементы матрицы решений накладываются следующие ограничения:

Т.е. каждый элемент может быть расположен только в одном блоке.

 

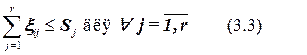Число элементов в блоке должно быть не больше заданного.


Выведем формулу для числа внешних выводов блока.

Очевидно, что выражение означает число межблочных связей, которые выходят из блока bj от элемента ei на элемент ek,расположенный вне блока bj.

Очевидно, что выражение означает число межблочных связей, выходящих из блока bj от элемента ei на все остальные элементы схемы, расположенные вне блока bj, включая элемент e0.

Для того, чтобы получить общее число выводов от блока bj, необходимо просуммировать предыдущее выражение по i:

Теперь получим формулу для суммарного числа межблочных связей:

С учетом выражения (3.2) второй член выражения (3.5) перепишем в виде:

– число связей с внешним разъемом схемы.

Поэтому в качестве можно взять первую часть целевой функции (3.5). Т.о., необходимо найти такую матрицу решений ξ, удовлетворяющую ограничениям (3.2)–(3.4), для которой обеспечивается минимум целевой функции (3.5). Данная задача является задачей квадратичного целочисленного программирования с булевыми переменными cij.

В связи с тем, что модель ВНГ является грубой моделью, то и полученные формулы (3.4), (3.5) носят грубый характер.

Для примера рассмотрим схему, приведенную на рисунке 3.1.

Рис. 3.1

ВНГ для данной схемы приведен на рисунке 3.2 (примечание: вес ребра на рисунке обозначен количеством связей).

Пусть требуется разбить приведенную схему на блоки с ограничениями:

.

Из рассмотрения ВНГ нетрудно видеть, что по данной модели невозможно разбить схему не только на два, но и на четыре блока. На самом же деле это не так (см. схему). Это говорит о неточности данной модели.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)