Алгоритм Прима

Использует тот же принцип соединения ближайших вершин, что и алг. Краскала, но на каждом шаге к строящемосю дереву присоед-ся ближайшая изолированная вершина.

В основе лежат 2 теоремы:

T.1. Каждая вершина КСД непосредственно связана по крайней мере с 1 ближайшей вершиной.

Т.2. Каждый измеряемый фрагмент поддерева связан по крайней мере с 1 из излир-х фрагментов кратчайшим ребром.

В соответствии с Т.1. построение КСД м.б. начато с произвольной вершины графа:

1) Выбираем, например, x1 и находим кратчайшее ребро, инертное этой. Это б. ребро .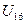

2) Включаем в КСД, вычеркиваем 1 и 6 столбцы (чтобы не было циклов), помечаем 6 строку и выбираем из нее минимальный элемент .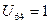

3) Включаем в КСД 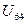, вычеркиваем 4 столбец, помечаем 4 строку и выбираем из нее минимальный элемент 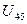=1.

4) Включаем в КСД 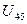, помечаем строку 5, вычеркиваем 5 столбец, выбираем 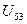=5.

5) Включаем в КСД, вычеркиваем 3 столбец, помечаем 3 строку и выбираем из неё 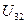=1.

КСД построено.

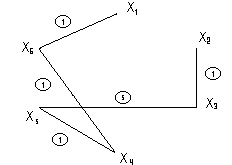Т.о. на Т шаге алг-ма исп. Т1, и далее Т2.

Здесь всегда Т компонента связности, т.е. Т разрастается по дереву.

Алгоритм Прима построения КСД при огран-х на лок-е степени вершины.

Лок. степени b 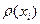- число ребер графа, инцидентных этой b. Т.к. задача возникает при проектировании проводных соединений, когда ограничено число паек к 1 контакту. Чаще всего кол. паек к контакту = 2.

предположим, что зад. матрица U длины ребер графа цепи и необходимо построить КСД при .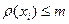

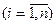Для решения дан. задачи м. применить алг. Прима с вычеркиванием строки, соответ-ей вершине лок. степени кот. стан. =n.

Пр:

Поиск по сайту: