Второй уровень сложности

Решить поставленную задачу с использованием рекурсивной и обычной функций. Сравнить полученные результаты.

1. Для заданного целого десятичного числа N получить его представление в p -ичной системе счисления (p < 10).

2. В упорядоченном массиве целых чисел a_i (i= 1,..., n)найти номер находящегося в массиве элемента c,используя метод двоичного поиска.

3. Найти наибольший общий делитель чисел M и N, используя теорему Эйлера: если M делится на N, то НОД (N, M)= N, иначе НОД (N, M)= (M mod N, N).

4. Числа Фибоначчи определяются следующим образом: Fb (0) = 0; Fb (1) = 1; Fb (n) = Fb (n -1) + Fb (n -2). Определить Fb (n).

5. Найти значение функции Аккермана A (m, n), которая определяется для всех неотрицательных целых аргументов m и n следующим образом:

A (0, n) = n + 1;

A (m, 0) = A (m -1, 1); при m > 0;

A (m, n) = A (m -1, A (m, n -1)); при m > 0 и n > 0.

6. Найти методом деления отрезка пополам минимум функции f (x) = = 7sin²(x) на отрезке [2, 6] с заданной точностью e (например 0.01).

7. Вычислить значение x = 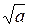, используя рекуррентную формулу x_n = = 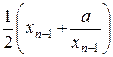, в качестве начального значения использовать x ₀ = 0,5(1 + a).

8. Найти максимальный элемент в массиве a_i (i= 1, ¼, n), используя очевидное соотношение max (a ₁, ¼, a_n) = max [ max (a ₁, ¼, a_{n -1}), a_n ].

9. Вычислить значение y (n) = .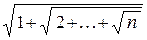

10. Найти максимальный элемент в массиве a_i (i= 1, ¼, n), используя соотношение (деления пополам) max (a ₁,¼, a_n) = max [ max (a ₁,¼, a_{n /2}), max (a_{n /2+1}, ¼, a_n)].

11. Вычислить значение y (n) = .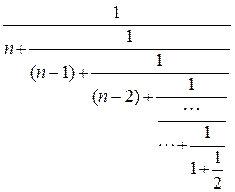

12. Вычислить произведение четного количества n (n ³ 2) сомножителей следующего вида y = ….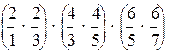

13. Вычислить y = xⁿ по следующему правилу: y = (x^{n/ 2} )², если n четное и y = x × y^{n -1}, если n нечетное.

14. Вычислить значение 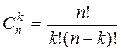(значение 0! = 1).

15. Вычислить y (n) = 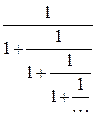, n задает число ступеней.

Поиск по сайту: