B15 (высокий уровень, время – 10 мин)

Тема: Преобразование логических выражений.

Пример задания:

Сколько различных решений имеет система логических уравнений

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄)= 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) = 1

(Øy₁ Ú x₁) Ù (Øy₂ Ú x₂) Ù (Øy₃ Ú x₃) Ù (Øy₄ Ú x₄) = 1

где x₁, x₂, …, x₄ и y₁, y₂, …, y₄ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение:

1) видим, что первые два уравнения независимы друг от друга (в первое входят только x₁, x₂, …, x₄, а во второе – только y₁, y₂, …, y₄)

2) третье уравнение связывает первые два, поэтому можно поступить так:

· найти решения первого уравнения

· найти решения второго уравнения

· найти множество решений первых двух уравнений

· из множества решений первых двух уравнений выкинуть те, которые не удовлетворяют последнему уравнению

3) найдем решения первого уравнения; каждая из логических переменных x₁, x₂, …, x₄ может принимать только два значения: «ложь» (0) и «истина» (1), поэтому решение первого уравнения можно записать как битовую цепочку длиной 4 бита: например, 0011 означает, что
x₁ = x₂ = 0 и x₃ = x₄ = 1

4) вспомним, что импликация x₁®x₂ ложна только для x₁ = 1 и x₂ = 0, поэтому битовая цепочка, представляющая собой решение первого уравнения, не должна содержать сочетания «10»; это дает такие решения (других нет!):

(x₁, x₂, x₃, x₄) = 0000 0001 0011 0111 1111

5) видим, что второе уравнение полностью совпадает по форме с первым, поэтому все его решения:

(y₁, y₂, y₃, y₄) = 0000 0001 0011 0111 1111

6) поскольку первые два уравнения независимы друг от друга, система из первых двух уравнений имеет 5·5=25 решений: каждому решению первого соответствует 5 разных комбинаций переменных y₁, y₂, …, y₄, которые решают второе, и наоборот, каждому решению второго соответствует 5 разных комбинаций переменных x₁, x₂, …, x₄, которые решают первое:

(y₁, y₂, y₃, y₄) = 0000 0001 0011 0111 1111

(x₁, x₂, x₃, x₄) = 0000 0000 0000 0000 0000

0001 0001 0001 0001 0001

0011 0011 0011 0011 0011

0111 0111 0111 0111 0111

1111 1111 1111 1111 1111

7) теперь проверим, какие ограничения накладывает третье уравнение; вспомнив формулу, которая представляет импликацию через операции «НЕ» и «ИЛИ» (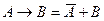), можно переписать третье уравнение в виде

(y₁ ® x₁) Ù (y₂ ® x₂) Ù (y₃ ® x₃) Ù (y₄ ® x₄) = 1

8) импликация y₁®x₁ ложна только для y₁ = 1 и x₁ = 0, следовательно, такая комбинация запрещена, потому что нарушает третье уравнение; таким образом, набору с y₁ = 1:

(y₁, y₂, y₃, y₄) = 1111

соответствует, с учетом третьего уравнения, только одно решение первого, в котором x₁ = 1

(y₁, y₂, y₃, y₄) = 1111

поэтому множество решений «редеет»:

(y₁, y₂, y₃, y₄) = 0000 0001 0011 0111 1111

(x₁, x₂, x₃, x₄) = 0000 0000 0000 0000

0001 0001 0001 0001

0011 0011 0011 0011

0111 0111 0111 0111

1111 1111 1111 1111 1111

9) аналогично двигаемся дальше по третьему уравнению; второй сомножитель равен 0, если импликация y₂®x₂ ложна, то есть только для y₂ = 1 и x₂ = 0, это «прореживает» предпоследний столбец:

(y₁, y₂, y₃, y₄) = 0000 0001 0011 0111 1111

(x₁, x₂, x₃, x₄) = 0000 0000 0000

0001 0001 0001

0011 0011 0011

0111 0111 0111 0111

1111 1111 1111 1111 1111

10) аналогично проверяем еще два ограничения, отбрасывая все решения, для которых y₃ = 1 и x₃ = 0, а также все решения, для которых y₄ = 1 и x₄ = 0:

(y₁, y₂, y₃, y₄) = 0000 0001 0011 0111 1111

(x₁, x₂, x₃, x₄) = 0000

0001 0001

0011 0011 0011

0111 0111 0111 0111

1111 1111 1111 1111 1111

11) итак, остается одно решение при (y₁, y₂, y₃, y₄)=1111, два решения при (y₁, y₂, y₃, y₄)=0111, три решения при (y₁, y₂, y₃, y₄)=0011, четыре решения при (y₁, y₂, y₃, y₄)=0001 и 5 решений при (y₁, y₂, y₃, y₄)=0000

12) всего решений 1+2+3+4+5=15.

Еще пример задания:

Сколько различных решений имеет система уравнений

(X₁ÙX₂) Ú (X₁ÙX₂) Ú (X₃ÙX₄) Ú (X₃ÙX₄) = 1

(X₃ÙX₄) Ú (X₃ÙX₄) Ú (X₅ÙX₆) Ú (X₅ÙX₆) = 1

(X₅ÙX₆) Ú (X₅ÙX₆) Ú (X₇ÙX₈) Ú (X₇ÙX₈) = 1

(X₇ÙX₈) Ú (X₇ÙX₈) Ú (X₉ÙX₁₀) Ú (X₉ÙX₁₀) = 1

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение:

1) количество комбинаций 10 логических переменных равно 2¹⁰ = 1024, поэтому вариант с построением полной таблицы истинности отпадает сразу

2) решать такую систему «в лоб» достаточно сложно, нужно попробовать ее упростить

3) заметим, что

(X₁ÙX₂) Ú (X₁ÙX₂) = (X₁ º X₂),

где символ º означает операцию «эквивалентность» (значения равны);

4) кроме того,

(X₃ÙX₄) Ú (X₃ÙX₄) = (X₃ Å X₄) = (X₃ º X₄),

где символ Å означает операцию «исключающее ИЛИ» (значения НЕ равны); это операция, обратная эквивалентности

5) используем замену переменных, выделив члены, объединяющие пары исходных переменных (X₁ и X₂, X₃ и X₄, X₅ и X₆, X₇ и X₈, X₉ и X₁₀)

Y₁ = (X₁ º X₂) Y₂ = (X₃ º X₄)

Y₃ = (X₅ º X₆) Y₄ = (X₇ º X₈)

Y₅ = (X₉ º X₁₀)

6) при этих обозначения система уравнений преобразуется к виду

Y₁ Ú Y₂ = 1

Y₂ Ú Y₃ = 1

Y₃ Ú Y₄ = 1

Y₄ Ú Y₅ = 1

1) такая система имеет 5+1 = 6 решений для независимых переменных Y₁ … Y₅

2) предположим, что значение Y₁ известно (0 или 1); поскольку 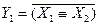, по таблице истинности операции «эквивалентность» есть две соответствующих пары (X₁;X₂) (как для случая Y₁ = 0, так и для случая Y₁ = 1)

3) у нас есть 5 переменных Y₁ … Y_5, каждая их комбинация дает 2 пары (X₁;X₂), 2 пары (X₃;X₄), 2 пары (X₅;X₆), 2 пары (X₇;X₈) и 2 пары (X₉;X₁₀), то есть всего 2⁵ = 32 комбинации исходных переменных

4) таким образом, общее количество решений равно 6 ·32 = 192

7) ответ: 192 решения

Задачи для тренировки:

1) Каково наибольшее целое число X, при котором истинно высказывание

(90 < X·X) → (X < (X-1))

2) Сколько различных решений имеет уравнение

(K Ù L Ù M) Ú (L Ù M Ù N) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

3) Укажите значения переменных K, L, M, N, при которых логическое выражение

(K Ú M) → (L Ú M Ú N)

ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

4) Каково наименьшее целое положительное число X, при котором высказывание:

(4 > -(4 + X)·X) → (30 > X·X)

будет ложным.

5) Каково наибольшее целое положительное число X, при котором истинно высказывание:

((X - 1) < X) → (40 > X·X)

6) Укажите значения переменных K, L, M, N, при которых логическое выражение

((M Ú L) Ù K) → ((K Ù M) Ú N)

ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

7) Каково наименьшее натуральное число X, при котором высказывание

(X·X < 9) → (X >(X + 2))

будет ложным?

8) Укажите значения логических переменных Р, Q, S, Т, при которых логическое выражение

(Р Ú Q) Ú (Q → (S Ú Т))

ложно. Ответ запишите в виде строки из четырех символов: значений переменных Р, Q, S, T (в указанном порядке).

9) Каково наибольшее целое положительное число X, при котором высказывание:

((X + 6)·X + 9 > 0) → (X·X > 20)

будет ложным?

10) Составьте таблицу истинности для логической функции

X = (А → B) Ù (C ↔ (B Ú A))

в которой столбец значений аргумента А представляет собой двоичную запись числа 226, столбец значений аргумента В – числа 154, столбец значений аргумента С – числа 75. Число в столбце записывается сверху вниз от старшего разряда к младшему. Переведите полученную двоичную запись значений функции X в десятичную систему счисления.

11) Составьте таблицу истинности для логической функции

X = (А → B) Ù (B ↔ (C → A))

в которой столбец значений аргумента А представляет собой двоичную запись числа 216, столбец значений аргумента В – числа 30, столбец значений аргумента С – числа 170. Число в столбце записывается сверху вниз от старшего разряда к младшему. Переведите полученную двоичную запись значений функции X в десятичную систему счисления.

12) Известно, что для чисел X, Y и Z истинно высказывание

(Z < X Ú Z < Y) Ù (Z+1 < X)Ù (Z+1 < Y)

Чему равно Z, если X=25 и Y=48?

13) Укажите значения переменных K, L, M, N, при которых логическое выражение

(K → M) Ú (L Ù K) Ú N

ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

14) Укажите значения переменных K, L, M, N, при которых логическое выражение

(K → M) Ù(K → M) Ù (K → (M Ù L Ù N))

истинно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

15) A, B и C – целые числа, для которых истинно высказывание:

(C<A Ú C<B) Ù (C+1 < A) Ù (C+1 < B)

Чему равно C, если A=45 и B=18?

16) Сколько различных решений имеет уравнение

J Ù K Ù L Ù M Ù (N Ú N) = 0

где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

17) A, B и С – целые числа, для которых истинно высказывание

(А = B) Ù ((B < A) → (2C > A)) Ù ((A < B) → (A > 2C))

Чему равно A, если C = 8 и B = 18?.

18) Сколько различных решений имеет уравнение

(K Ù L) Ú (M Ù N) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

19) Каково наибольшее целое положительное число X, при котором истинно высказывание:

(X·X - 1 > 100) → (X·(X-1)< 100)

20) Каково наибольшее целое положительное число X, при котором ложно высказывание:

(8·X - 6 < 75) → (X·(X-1)> 65)

21) Каково наибольшее целое положительное число X, при котором ложно высказывание:

(X·(X+1) > 55) → (X·X > 50)

22) Каково наибольшее целое положительное число X, при котором истинно высказывание:

(X·(X+1) > X·X + 7) → (X·(X+1) ≤ X·X + 7)

23) Сколько различных решений имеет уравнение

(K Ú L Ú M) Ù (L Ù M Ù N) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

24) Сколько различных решений имеет уравнение

(K Ù L Ù M) → (M Ù N) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

25) Сколько различных решений имеет уравнение

(K Ú L)Ù(M Ú N) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

26) Сколько различных решений имеет уравнение

((A → B)Ù C) Ú (D Ù D)= 1,

где A, B, C, D – логические переменные? В ответе не нужно перечислять все различные наборы значений A, B, C, D, при которых выполнено данное равенство. В качестве ответа вам нужно указать количество таких наборов.

27) Каково наибольшее целое положительное число X, при котором ложно высказывание:

(X·(X + 1)> 55) → (X·X > 50)

28) Каково наибольшее целое положительное число X, при котором истинно высказывание:

(X·(X + 1) > X·X + 7) → (X·(X + 1) ≤ X·X + 7)

29) Каково наибольшее целое положительное число X, при котором истинно высказывание:

(X·X - 7 > 15) → (X·X + 8 < 35)

30) Каково наибольшее целое положительное число X, при котором ложно высказывание:

(9·X + 5 > 60) → (X·X > 80)

31) Сколько различных решений имеет уравнение

M Ù K Ù N Ù J Ù(L Ú L) = 0

где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

32) Каково наибольшее целое число X, при котором истинно высказывание:

(X·X - 1 > 100) → (X·(X – 1) < 100)

33) Укажите значения переменных K, L, M, N, при которых логическое выражение

(K → M) Ú (L Ù M Ù K) Ú N

ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

34) Сколько различных решений имеет уравнение

(K Ú L Ú M) Ù (L Ú M Ú N) = 0

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

35) Сколько различных решений имеет уравнение

((J → K) → (M Ù N)) Ù ((J Ù K) → (M Ú N)) Ù (M Ú N Ú K Ú L)=1

где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

36) Сколько различных решений имеет уравнение

((J Ú K Ú L) → (M → N)) Ù ((J Ù K Ù L) → (M Ú N)) Ù (M Ú N Ú K)=1

где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

37) Сколько различных решений имеет уравнение

((J → K) → (L Ù M Ù N)) Ú ((L Ù M Ù N) → (J Ú K)) Ú (M Ù J)=0

где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

38) Укажите значения переменных K, L, M, N, при которых логическое выражение

((M Ú L) Ù K) → ((K Ù M) Ú N)

ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

39) Сколько различных решений имеет уравнение

(((K Ù L Ù N) → (L → M)) Ú ((K Ú L Ú N) → (L Ù M))) Ù (K Ú N) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

40) Сколько различных решений имеет уравнение

(((K → M) → (M Ù L Ù N)) Ú ((K Ù M) → (M Ú L Ú N))) Ù (L Ù M) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

41) A, B и С – целые числа, для которых истинно высказывание

(А = B) Ù ((A > B) → (C = B)) Ù ((B > A) → (C = A))

Чему равно B, если A = 45 и C = 18?.

42) Сколько различных решений имеет уравнение

(X Ú Y Ú Z) → (X Ù P) = 1

где X, Y, Z, P – логические переменные? В ответе не нужно перечислять все различные наборы значений, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

43) Каково наименьшее целое положительное число X, при котором ложно высказывание:

(82 < X·X) → (81 > (X-1)·(X-1))

44) Сколько различных решений имеет уравнение

(X Ù Y Ú Z) → (Z Ú P) = 0

где X, Y, Z, P – логические переменные? В ответе не нужно перечислять все различные наборы значений, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

45) Каково наименьшее натуральное число X, при котором истинно высказывание:

(X·(X+1) < 50) → (X·X > 35)

46) Каково наибольшее натуральное число X, при котором истинно высказывание:

(X·(X + 1) > 99) → (X·X < 65)

47) Сколько существует целых значений X, при которых ложно высказывание:

(|X| ≥ 5) Ú (|X| < 1)

48) Сколько существует целых значений X, при которых ложно высказывание:

((|X| < 5) Ù (|X| < 1) Ù (|X| < 10))

49) Сколько существует целых значений X, при которых ложно высказывание:

((X-4)·(X-6) ≥ 0) → (X·X - 12·X + 35 > 0)

50) Сколько различных решений имеет уравнение

((K → L) Ù (M → N) → K) Ù (L → M) = 1

где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

51) Сколько различных решений имеет уравнение

(J → L) Ù (K → L) Ù (M → N) Ù (L → M) Ù (M → K) = 1

где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

52) Сколько различных решений имеет система уравнений

((X₁ º X₂) Ù (X₃ º X₄)) Ú ((X₁ º X₂) Ù (X₃ º X₄)) = 0

((X₃ º X₄) Ù (X₅ º X₆)) Ú ((X₃ º X₄) Ù (X₅ º X₆)) = 0

((X₅ º X₆) Ù (X₇ º X₈)) Ú ((X₅ º X₆) Ù (X₇ º X₈)) = 0

((X₇ º X₈) Ù (X₉ º X₁₀)) Ú ((X₇ º X₈) Ù (X₉ º X₁₀)) = 0

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

53) Сколько различных решений имеет система уравнений

(X₁ Ù X₂) Ú (X₁ Ù X₂) Ú (X₁ º X₃) = 1

(X₂ Ù X₃) Ú (X₂ Ù X₃) Ú (X₂ º X₄) = 1

...

(X₇ Ù X₈) Ú (X₇ Ù X₈) Ú (X₇ º X₉) = 1

(X₈ Ù X₉) Ú (X₈ Ù X₉) Ú (X₈ º X₁₀) = 0

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

54) Сколько различных решений имеет система уравнений

(X₁ Ù X₂) Ú (X₁ Ù X₂) Ú (X₂ Ù X₃) Ú (X₂ Ù X₃) = 1

(X₂ Ù X₃) Ú (X₂ Ù X₃) Ú (X₃ Ù X₄) Ú (X₃ Ù X₄) = 1

...

(X₇ Ù X₈) Ú (X₇ Ù X₈) Ú (X₈ Ù X₉) Ú (X₈ Ù X₉) = 1

(X₈ Ù X₉) Ú (X₈ Ù X₉) Ú (X₉ Ù X₁₀) Ú (X₉ Ù X₁₀) = 0

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

55) Сколько различных решений имеет система уравнений

(X₁ º X₂) Ú (X₁ Ù X₁₀) Ú (X₁ Ù X₁₀)= 1

(X₂ º X₃) Ú (X₂ Ù X₁₀) Ú (X₂ Ù X₁₀)= 1

...

(X₉ º X₁₀) Ú (X₉ Ù X₁₀) Ú (X₉ Ù X₁₀)= 1

(X₁ º X₁₀) = 0

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

56) Сколько различных решений имеет система уравнений

((X₁ º X₂) Ú (X₃ º X₄)) Ù ((X₁ º X₂) Ú (X₃ º X₄)) = 1

((X₃ º X₄) Ú (X₅ º X₆)) Ù ((X₃ º X₄) Ú (X₅ º X₆)) = 1

((X₅ º X₆) Ú (X₇ º X₈)) Ù ((X₅ º X₆) Ú (X₇ º X₈)) = 1

((X₇ º X₈) Ú (X₉ º X₁₀)) Ù ((X₇ º X₈) Ú (X₉ º X₁₀)) = 1

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

57) Сколько различных решений имеет система уравнений

(X₁ º X₂) Ù (X₂ º X₃) = 1

(X₂ º X₃) Ù (X₃ º X₄) = 1

...

(X₈ º X₉) Ù (X₉ º X₁₀) = 1

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

58) Сколько различных решений имеет логическое уравнение

(X₁ Ú X₂) Ù(X₂ Ú X₃) Ù(X₃ Ú X₄) Ù(X₄ Ú X₅) Ù(X₅ Ú X₆)= 1

где x₁, x₂, …, x₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

59) Сколько различных решений имеет система уравнений

(X₁ Ù X₂ Ù X₃) Ú (X₁ Ù X₂ Ù X₃) Ú (X₁ Ù X₂ Ù X₃) = 1

(X₂ Ù X₃ Ù X₄) Ú (X₂ Ù X₃ Ù X₄) Ú (X₂ Ù X₃ Ù X₄) = 1

...

(X₇ Ù X₈ Ù X₉) Ú (X₇ Ù X₈ Ù X₉) Ú (X₇ Ù X₈ Ù X₉) = 1

где x₁, x₂, …, x₉ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

60) (http://ege.yandex.ru/informatics) Сколько различных решений имеет система уравнений?

(x₁ ® x₂)Ù(x₂ ® x₃)Ù(x₃ ® x₄)Ù(x₄ ® x₅) = 1

(у₁ ® у₂)Ù(у₂ ® у₃)Ù(у₃ ® у₄)Ù(у₄ ® у₅) = 1

x₁ Ú у₁ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

61) (С.Э. Назаренко, МОУ СОШ №7 г.Ноябрьска) Сколько различных решений имеет система уравнений?

(Øx₁ ® x₂)Ù(Øx₂ ® x₃)Ù(Øx₃ ® x₄)Ù(Øx₄ ® x₅) = 1

(Øу₁ ® у₂)Ù(Øу₂ ® у₃)Ù(Øу₃ ® у₄)Ù(Øу₄ ® у₅)= 1

x₁ Ú у₁ = 0

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

62) (С.Э. Назаренко) Сколько различных решений имеет система уравнений?

(Øx₁ ® Øx₂)Ù(x₂ ® x₃)Ù(Øx₃ ® Øx₄)Ù(x₄ ® x₅)=1

(Øу₁ ® Øу₂)Ù(у₂ ® у₃)Ù(Øу₃ ® Øу₄)Ù(у₄ ® у₅)=1

x₁ Ù у₁ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

63) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅)=1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅)=1

x₅ Ù у₅ = 0

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

64) Сколько различных решений имеет система уравнений?

x₁ Ú Øx₂ Ú Øx₃ Ù x₄ = 1

x₃ Ú Øx₄ Ú Øx₅ Ù x₆ = 1

x₅ Ú Øx₆ Ú Øx₇ Ù x₈ = 1

x₇ Ú Øx₈ Ú Øx₉ Ù x₁₀ = 1

где x₁,x₂,…,x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

65) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ú x₃ Ù Øx₄ = 1

(x₃ ® x₄) Ú x₅ Ù Øx₆ = 1

(x₅ ® x₆) Ú x₇ Ù Øx₈ = 1

(x₇ ® x₈) Ú x₉ Ù Øx₁₀ = 1

(x₉ ® x₁₀) Ú x₁ Ù Øx₂ = 1

где x₁,x₂,…,x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

66) Сколько различных решений имеет логическое уравнение

(X₁®X₂) Ù (X₂®X₃) Ù (X₃®X₄) Ù (X₄®X₅) Ù (X₅®X₁) = 1

где x₁,x₂,…,x₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

67) Сколько различных решений имеет логическое уравнение

(X₁®X₂) Ù (X₂®X₃) Ù (X₃®X₄) Ù (X₄®X₅) Ù (X₅®ØX₁) = 1

где x₁,x₂,…,x₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

68) (http://ege.yandex.ru) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₅ ® у₄) Ù (у₄ ® у₃) Ù (у₃ ® у₂) Ù (у₂ ® у₁) = 1

x₃ Ù у₃ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

69) (http://ege.yandex.ru) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) = 1

x₁ ® у₁ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

70) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₅ ® у₄) Ù (у₄ ® у₃) Ù (у₃ ® у₂) Ù (у₂ ® у₁) = 1

x₁ ® у₁ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

71) (http://ege.yandex.ru) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) = 1

(x₁ ® y₁) Ù (x₂ ® y₂) = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

72) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) = 1

(x₁ ® y₁) Ù (x₂ ® y₂) Ù (x₃ ® y₃) = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

73) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) = 1

(x₁ ® y₁) Ù (x₂ ® y₂) Ù (x₃ ® y₃) Ù (x₄ ® y₄) = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

74) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ ® x₆ = 1

y₁ ® y₂ ® y₃ ® y₄ ® y₅ ® y₆ = 1

где x₁,x₂,…,x_6, у₁,у₂,…,у₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

75) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ = 1

y₁ ® y₂ ® y₃ ® y₄ ® y₅ = 0

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

76) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ = 0

y₁ ® y₂ ® y₃ ® y₄ = 1

z₁ ® z₂ ® z₃ ® z₄ = 0

где x₁,x₂,…,x_4, у₁,у₂,…,у_4, z₁,z₂,…,z₄ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

77) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ ® x₆ = 1

y₁ ® y₂ ® y₃ ® y₄ ® y₅ ® y₆ = 1

x₁ ® y₁ = 1

где x₁,x₂,…,x_6, у₁,у₂,…,у₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

78) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ = 1

y₁ ® y₂ ® y₃ ® y₄ ® y₅ = 1

x₁ ® y₅ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

79) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ = 1

y₁ ® y₂ ® y₃ ® y₄ ® y₅ = 0

x₁ ® y₅ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

80) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ = 0

y₁ ® y₂ ® y₃ ® y₄ ® y₅ = 0

x₁ ® y₅ = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

81) Сколько различных решений имеет система уравнений?

x₁ ® x₂ ® x₃ ® x₄ ® x₅ ® x₆ = 1

y₁ ® y₂ ® y₃ ® y₄ ® y₅ ® y₆ = 1

x₁ ® y₆ = 0

y₁ ® x₆ = 0

где x₁,x₂,…,x_6, у₁,у₂,…,у₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

82) Сколько различных решений имеет система уравнений

(X₁ Ú X₂) Ù (ØX₃ Ú ØX₄) = 0

(X₃ Ú X₄) Ù (ØX₅ Ú ØX₆) = 0

(X₅ Ú X₆) Ù (ØX₇ Ú ØX₈) = 0

(X₇ Ú X₈) Ù (ØX₉ Ú ØX₁₀) = 0

где x₁, x₂, …, x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

83) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) = 1

(Øy₁ ® x₁) Ù (Øy₂ ® x₂) Ù (Øy₃ ® x₃) Ù (Øy₄ ® x₄) Ù (Øy₅ ® x₅) = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

84) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) = 1

(Øy₁ Ú x₁) Ù (Øy₂ Ú x₂) Ù (Øy₃ Ú x₃) Ù (Øy₄ Ú x₄) Ù (Øy₅ Ú x₅) = 1

где x₁,x₂,…,x_5, у₁,у₂,…,у₅ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

85) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) Ù (x₅ ® x₆) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) Ù (у₅ ® у₆) = 1

(Øy₁ Ú x₁) Ù (Øy₂ Ú x₂) Ù (Øy₃ Ú x₃) Ù (Øy₄ Ú x₄) Ù (Øy₅ Ú x₅) Ù (Øy₆ Ú x₆) = 1

где x₁,x₂,…,x_6, у₁,у₂,…,у₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

86) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) Ù (x₅ ® x₆) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) Ù (у₄ ® у₅) Ù (у₅ ® у₆) = 1

(Øy₁ Ú x₁) Ù (Øy₂ Ú x₂) Ù (Øy₃ Ú x₃) Ù (Øy₄ Ú x₄) Ù (Øy₅ Ú x₅) Ù (Øy₆ Ú x₆) = 0

где x₁,x₂,…,x_6, у₁,у₂,…,у₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

87) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) Ù (x₄ ® x₅) Ù (x₅ ® x₆) = 1

(x₁ ® Øу₁) Ù (x₂ ® Øу₂) Ù (x₃ ® Øу₃) Ù (x₄ ® Øу₄) Ù (x₅ ® Øу₅) Ù (x₆ ® Øу₆) = 1

где x₁,x₂,…,x_6, у₁,у₂,…,у₆ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

88) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) = 1

(Øy₁ Ú x₁) Ù (Øy₂ Ú x₂) Ù (Øy₃ Ú x₃) Ù (Øy₄ Ú x₄) = 1

где x₁,x₂,…,x_4, у₁,у₂,…,у₄ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

89) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) = 1

(Øy₁ Ú x₁) Ù (Øx₂ Ú y₂) Ù (Øy₃ Ú x₃) Ù (Øx₄ Ú y₄) = 1

где x₁,x₂,…,x_4, у₁,у₂,…,у₄ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

90) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) = 1

(Øy₁ Ú x₁) Ù (Øx₂ Ú y₂) = 1

где x₁,x₂,…,x_4, у₁,у₂,…,у₄ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

91) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ù (x₂ ® x₃) Ù (x₃ ® x₄) = 1

(у₁ ® у₂) Ù (у₂ ® у₃) Ù (у₃ ® у₄) = 1

(Øy₁ Ú x₁) Ù (Øy₂ Ú x₂) = 1

где x₁,x₂,…,x_4, у₁,у₂,…,у₄ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Поиск по сайту: