 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
а) Находим границы, в которых с вероятностью 0,9946 заключено среднее время обслуживания всех клиентов пенсионного фонда
По таблицам значений функции Лапласа находим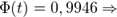 
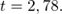
Интервальные оценки для средней находятся по формулам при объеме выборки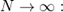 
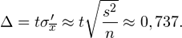
Искомые границы определяются двойным неравенством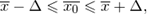 
то есть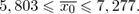 
б) Находим среднюю квадратическую ошибку выборки для доли. С учетом того, что число клиентов очень велико, объем генеральной совокупности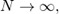 
поэтому формула принимает вид (для бесповторной выборки):
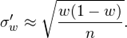
Здесь 
выборочная доля клиентов в выборке, время обслуживания которых составило меньше 6 минут:
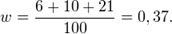
Тогда в нашем случае получаем:
Ищем вероятность того, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).
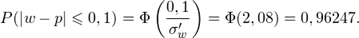
в) Ищем объем повторной выборки, при котором с вероятностью 0,9907 можно утверждать, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).
В качестве неизвестного значения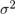 
для определения объема выборки берем его состоятельную оценку 
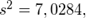найденную ранее. Учитывая, что 
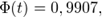по таблице значений функции Лапласа определяем, что 
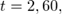и объем повторной выборки равен:
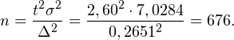
5. Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице.
| y x | 5–9 | 9–13 | 13–17 | 17–21 | 21–25 | Итого |
| 15–21 | ||||||
| 21–27 | ||||||
| 27–33 | ||||||
| 33–39 | ||||||
| 39–45 | ||||||
| 45–51 | ||||||
| Итого |
Необходимо:
1. Вычислить групповые средние 
, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить средний рост производительности труда при степени автоматизации производства 43%.
Решение:
1. Находим групповые средние по формулам:
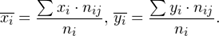
Здесь 
и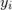 
— середины соответствующих интервалов:
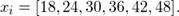
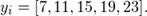
Пример вычислений групповых средних:
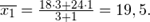
Полученные значения заносим в таблицу:
| Групповые средние по Y | ||||||
| 9,667 | ||||||
| 15,333 | ||||||
| 16,6 | ||||||
| 18,2 | ||||||
| Групповые средние по X | 19,5 | 31,333 | 35,647 |
2. Отвечаем на оставшиеся вопросы.
a) Для нахождения уравнений регрессии вычисляем необходимые суммы:
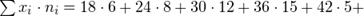
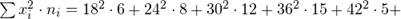
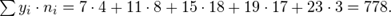
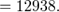
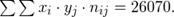
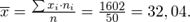
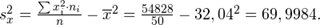
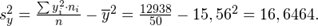
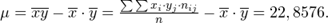
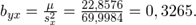
Искомые линии регрессии тогда имеют вид:
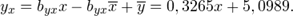
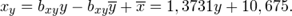
б) Находим коэффициент корреляции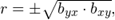 
радикал берем с плюсом, поскольку коэффициенты 
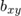и 
положительны:
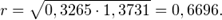
Оцениваем коэффициент значимости корреляции:
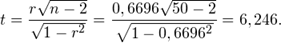
По таблице значений критерия Стьюдента для уровня значимости в 
находим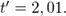 
Так как 
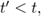коэффициент значимости значительно отличается от нуля, делаем вывод, что связь тесная и прямая.
в) По найденному уравнению регрессии оцениваем рост производительности труда при степени автоматизации производства 43 %:
%.
Поиск по сайту: