По дисциплине

«Теория вероятностей и математическая статистика»

для студентов бакалавриата II курса всех направлений

На 2013/2014 уч. год

ВАРИАНТ 1

(для студентов, номера личных дел которых оканчиваются цифрой 1)

1. Из 40 вопросов курса высшей математики студент знает 32. На экзамене ему случайным образом предлагаются два вопроса.

Какова вероятность того, что студент ответит правильно:

а) хотя бы на один вопрос;

б) на оба вопроса?

Решение:

Под случайным событием в данной задаче понимается получение студентом двух вопросов на экзамене. Вопросы повторяться не могут и порядок их следования в билете не важен. Тогда общее число возможных исходов данного события определяется число сочетаний из 40 элементов по 2 и вычисляется по формуле:

а) Рассчитаем вероятность того, что студенту попадется в билете два вопроса из тех, которые он не знает. Вновь имеем дело с сочетаниями 8 элементов по 2, число которых определяется по формуле:

Тогда вероятность такого события равна 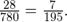Тогда вероятность противоположного события, заключающегося в том, что студенту попадется хотя бы один вопрос, который он знает, равна:

б) Ищем теперь вероятность того, что студенту попадутся оба вопроса из тех, что он знает. Имеем дело с сочетаниями из 32 элементов по 2, число которых определяется по формуле:

Тогда вероятность этого события равна

2. Человек, проходящий мимо киоска, покупает газету с вероятностью 0,2.

Найти вероятность того, что из 400 человек, прошедших мимо киоска в течение часа:

а) купят газету 90 человек;

б) не купят газету от 300 до 340 человек (включительно).

Решение:

а) Имеем m=90, n=200>100, q=1-0,2=0,8, тогда npq=400·0,2·0,8=64>20, следовательно в расчетах можно использовать локальную и интегральную теоремы Муавра-Лапласа.

Искомая вероятность равна:

б) Ищем вероятность того, что газеты не купят, поэтому в данном случае

n=400, p=0,8, q =1-0,8=0,2

Получаем тогда:

Тогда получаем, что искомая вероятность равна (см. таблицу значений функции Лапласа):

3. Пульт охраны связан с тремя охраняемыми объектами. Вероятность поступления сигнала с этих объектов составляет 0,2, 0,3 и 0,6 соответственно. Составить закон распределения случайной величины – числа объектов, с которых поступит сигнал. Найти математическое ожидание и дисперсию этой случайной величины.

Решение:

Введем обозначения — события, заключающиеся в поступлении сигналов с первого, второго и третьего объектов соответственно. Тогда:

Контроль:

Закон распределения тогда принимает вид:

	0,224	0,488	0,252	0,036

Математическое ожидание вычисляем по формуле:

Дисперсию вычисляем по формуле:

4. С целью определения средней продолжительности обслуживания клиентов в пенсионном фонде, число клиентов которого очень велико, по схеме собственно-случайной бесповторной выборки проведено обследование 100 клиентов. Результаты обследования представлены в таблице.

Найти:

а) границы, в которых с вероятностью 0,9946 заключено среднее время обслуживания всех клиентов пенсионного фонда;

б) вероятность того, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 0,1 (по абсолютной величине);

в) объем повторной выборки, при котором с вероятностью 0,9907 можно утверждать, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).

Решение:

Находим выборочную среднюю:

Здесь: объем выборки, — середины интервалов. Крайние незамкнутые интервалы заменены интервалами соответствующей длины.

Находим выборочную дисперсию:

Поиск по сайту: