Алг «среднее значение»

массив X[1:N]

нач Результаты:

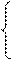от k = 1 до N цикл

кцикл [k = (1...N)]

Xcp:= S Xcp = S

Кон

Этот алгоритм обычно считается ошибочным (?!). «Ошибкой» в этом алгоритме считается отсутствие присваивания S:= 0 перед началом цикла.

Разберем результаты выполнения алгоритма на первых трех ша­гах:

S₁ = S₀×(l - 1)/1 + Х[1]/1 = S₀×0/1 + Х[1]/1 = Х[1]/1;

S₂ = S₁×(2 - 1)/2 + Х[2]/2 = S₁×1/2 + Х[2]/2 = Х[1]/2 + Х[2]/2;

S₃ = S₂×(3 - 1)/3 + Х[3]/3 = S₂×2/3 + Х[3]/3 = Х[1]/3 + Х[2]/3 + Х[3]/3.

Можно утверждать, что на первых трех шагах результатом является среднее арифметическое обрабатываемых чисел. На основе этих примеров можно сделать индуктивное утверждение - «на каждом очередном k-м шаге выполнения цикла результатом будет среднее арифметическое»

S_k = S_k-1×(k-l)/k + X[k]/k = X[l]/k + X[2]/k +... + X[k]/k.

Доказательство этого утверждения проводится с помощью мате­матической индукции. На первом шаге при k = 1 оно уже доказано. Допустим, что оно справедливо на (k -1)-м шаге

S_k-1 = X[l]/(k-l) + X[2]/(k-l) +... + X[k-l]/(k-l).

Подставим его в описание результатов цикла на k-м шаге

S_k= S_k-1×(k-l)/k +X[k]/k.

Тогда результат выполнения цикла на k-м шаге оказывается рав­ным

S_k = X[l]/k + X[2]/k +... + X[k-l]/k + X[k]/k,

т. е. среднему арифметическому первых k чисел.

Таким образом, индуктивное утверждение доказано. В силу мате­матической индукции это утверждение верно для всех k = l, 2,..., N. Следовательно, на последнем шаге конечным результатом выполнения цикла станет значение

S_N = S_N-1×(N-1) + X[N]/N = X[1]/N +... + X[N]/N.

Исходя из этого утверждения конечным результатом выполнения алгоритма в целом будет среднее арифметическое значение

Xcp = S_N = X[1]/N +... + X[N]/N.

Следовательно, приведенный алгоритм, несмотря на содержа­щуюся в нем «ошибку», является правильным. В целом анализ правильности алгоритмов с циклами во многом построен на исполь­зовании индукции.

Индукция - это вывод общих суждений из частных примеров. При анализе циклов она используется для подбора индуктивных утверждений о промежуточных результатах выполнения циклов. Однако для доказательства правильности индуктивных утверждений о результатах выполнения циклов используется полная математи­ческая индукция.

Математическая индукция - это принцип доказательства после­довательностей утверждений Р(1), Р(2), Р(3),..., P(N),.... когда известно, что верны первые утверждения для n = 1, 2, 3 и из истин­ности (n - 1)-го утверждения следует истинность n-го утверждения:

Принцип математической индукции: если первое утверждение Р(1) истинно и из утверждения Р(n - 1) следует утверждение Р(n), то истинны все утверждения Р(1), Р(2), Р(3),..., Р(n),....

Приведем примеры индуктивного анализа циклов для алгоритма нахождения минимального значения в последовательности чисел, который в этот раз действительно будет ошибочным.

Поиск по сайту: