АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка задачи. Упорядочение последовательности чисел

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. II. Основные задачи и функции
  4. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  5. II. Цель и задачи государственной политики в области развития инновационной системы
  6. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  7. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  8. Аналитические возможности, задачи и основные направления анализа СНС
  9. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА
  10. Билет 1. Предмет истории как науки: цели и задачи ее изучения
  11. Билет №17. Внутренняя политика Ивана IV Грозного. Задачи, этапы, итоги.
  12. Биофизика – как наука. Практические задачи. Методы исследования

Упорядочение последовательности чисел.

Дано: x1, х2,..., хN - исходные числа.

Треб.: x1', x2',..., хN' - упорядоченные числа.

Где: х1' £ х2' £... £ хN'.

При: N > 0.

Упорядочение чисел по методу «пузырька» в общей форме имеет вид:

Способ «упорядочение чисел»

нач

от k=1 до N-1 цикл

хтп:= xk

imn:= k

от i=k+1 до N цикл

если xi < хтп то

хтп:= xi

imn: = i

кесли

кцикл

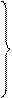xmn = Min (хk,..., хN)

xk' = хтп

ximn ' = xk

кцикл хk¢ = Min (хk,..., хN)

кон x1 < х2 <... < хk¢

 

Приведенный алгоритм можно рассматривать как алгоритм, сло­женный из нескольких фрагментов - вспомогательных алгоритмов, решающих определенные подзадачи.

Первый фрагмент (внутренний цикл) решает подзадачу нахожде­ния минимального значения в подмассиве x[k:N]. Второй фрагмент решает подзадачу перемещения k-го минимального значения на k-e место в массиве.

Лемма 1. Для вспомогательного алгоритма


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)