 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Программа. При отсутствии готовых программ для решения задач возникает проблема создания соответствующих алгоритмов и программ
¯
данные ® ЭВМ ® результаты
При отсутствии готовых программ для решения задач возникает проблема создания соответствующих алгоритмов и программ. В любом случае необходимо подобрать и определить способы, методы и средства для решения поставленных задач.
Систематический подход к составлению программ предполагает в качесте первого этапа составление спецификаций - описаний форм ввода и хранения данных в ЭВМ, а также получения и вывода результатов. Эти спецификации в дальнейшем будут использоваться для оценки правильности созданных программ.
Для диалоговых программ в роли таких спецификаций выступают сценарии диалога - полные описания результатов и правил работы с ЭВМ при решении поставленных задач. Только после создания таких спецификаций должны составляться соответствующие им алгоритмы и программы.
Составление программ
задача ® способы
¯ ¯
сценарий ® алгоритмы
¯ ¯
ЭВМ программа
Приведенная схема представляет основной принцип систематических методов составления алгоритмов и программ для решения различных прикладных задач - экономических, математических, физических, инженерных и т. д.
Особенностью систематических методов является возможность полного устранения ошибок из алгоритмов и программ. При этом подходе программы сверяются с описаниями алгоритмов, а алгоритмы - с описаниями сценариев и методов решения.
Такой систематический подход к составлению алгоритмов и программ может применяться к решению на ЭВМ любых прикладных задач с использованием самых различных языков программирования - Бейсик, Паскаль, Си и им подобные. Приведем примеры систематического решения задач.
Первая задача: подсчет площади треугольника по длинам сторон.
 a b
a b
c
Постановка Сценарий

Дано: а, b, с - длины сторон, площадь треугольника
Треб.: S - площадь треугольника, длины сторон:
 При: а > 0, b > 0, с > 0, а =? <а>
При: а > 0, b > 0, с > 0, а =? <а>
a < b +c, b < a + c, c < a + b. b =? <b>
с =? <с>
 |  |  | |||
Метод решения площадь = <S>
 S =
S =  недопустимы длины
недопустимы длины
р = (а + b + с)/2
Обратите внимание: в постановке задачи в исходные условия включены ситуации, когда решение может не существовать. А именно, здесь указаны три неравенства треугольника и условия положительности длин сторон. При нарушении этих условий треугольника просто не существует и тем более нельзя говорить о его площади.
Для надежности программ такого рода ситуации (когда нет решений) должны быть предусмотрены в сценарии диалога. В этих случаях в сценарий необходимо включить сообщения с диагностикой причин отказов: отсутствие решений, недопустимость данных, некорректность команд, противоречивость фактов и т. п.
Алгоритм Программа
алг «площадь треугольника» ' площадь треугольника
нач cls
вывод («площадь треугольника»)? «площадь треугольника»
вывод («длины сторон:»)? «длины сторон:»
запрос («а=», a) input «a=», a
запрос («b=», b) inpnt «b=», b
запрос («с=», с) input «c=», c
если не (а > 0 и b > 0 и с > 0) то if a<=0 or b<=0 or c<=0 then
вывод («недопустимы длины»)? «недопустимы длины»
инеc не (а < b + с и b < а + elseif not (a < b+ с and b < а + с
+с и с<а+b)то and с < а + b) then
вывод («недопустимы длины»)? «недопустимы длины»
иначе else
р:= (а + b + с)/2 р = (а+ b +с)/2
S := 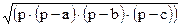 S = sqr (p*(p-a)*(p-b)*(p-c))
S = sqr (p*(p-a)*(p-b)*(p-c))
вывод («площадь=», S)? «площадь=», S
все end if
кон end
Рассмотренный пример служит иллюстрацией постановки задачи, в которой выделены как требуемые и исходные данные, так и условия допустимости исходных данных. Такая постановка задачи позволяет заранее выделить все случаи и ситуации недопустимости данных, что в дальнейшем понадобится при составлении сценария диалога с компьютером.
В общем случае математическая постановка задач должна содержать не только условия допустимости данных, но и точное описание требований к результатам:
1) дано: перечень исходных данных;
2) треб: перечень требуемых данных;
3) где: требования к результатам;
4) при: условия допустимости данных.
Вторая задача: определение среднего арифметического последовательности из N чисел х1, х2,..., хN. Приведем постановку, метод решения и сценарий диалога для решения этой задачи.
Постановка задачиСценарий

Дано: N - количество чисел, среднее N чисел
x1, х2,.., хN - числа, чисел =? <N>

 Треб.: s - среднее N чисел. *
Треб.: s - среднее N чисел. *
Где: s = (х1, + х2 +...+ хN)/ N. 1: <х1>
При: N > 0. 2: <х2>
………..
Метод решения N: <хN>
 |  |  | |||||
 | |||||||
 S0 = 0 среднее = <s>
S0 = 0 среднее = <s>
 Sk = Sk-1 + хk
Sk = Sk-1 + хk
[k = 1,..., N] недопустимо N
s = SN / N
Обратите внимание: метод вычисления среднего N чисел здесь описан через подсчет суммы чисел. Правильность метода может быть проверена по отношению к требованиям постановки задачи.
Приведем алгоритм и программу обработки данных, составленные в точном соответствии с выбранным сценарием и методом решения:
АлгоритмПрограмма
алг «среднее арифметическое» ' среднее арифметическое
нач cls
вывод («среднее N чисел»)? «среднее N чисел»
запрос («чисел=», N) input «чисел=», N
S:= 0 S = 0
если N <= 0 то if N <= 0 then
вывод («недопустимо N»)? «недопустимо N»
инеc N > 0 то elseif N > 0 then
от k = 1 до N цикл for k = 1 to N
вывод (k, «:»)? k, «:»
запрос (x) input x
S:= S + x S = S + x
кцикл next k
s:= S/N s = S/N
вывод («среднее =», s)? «среднее=», s
все end if
кон end
При решении сложных задач для проверки правильности составляемых алгоритмов и программ обязательны не только математическое описание постановки задач, но и описание выбранных методов решения.
Приведем пример разработки программы обработки данных с математической постановкой задачи и полным описанием метода решения.
Третья задача: определение самого легкого из учеников по данным из таблицы, содержащей N строк:
Поиск по сайту: