Основные свойства алгоритмов

Алгоритм относится к фундаментальным понятиям информатики. На понятии алгоритма построено все основные принципы програм­мирования - составления программ для вычислительных машин.

Алгоритм - это совокупность действий со строго определенными правилами выполнения. В информатике изучаются различного рода алгоритмы - диалоговые алгоритмы, алгоритмы обработки данных, вычислительные алгоритмы, алгоритмы управления роботами, стан­ками и другими техническими устройствами.

Пример диалогового алгоритма:

Алгоритм Блок-схема

алг «приветствие» ¯

нач запрос («Ваше имя=», NN)

запрос («Ваше имя=», NN) ¯

вывод («Добрый день», NN) вывод («Добрый день», NN)

кон ¯

Для описания алгоритмов используются блок-схемы, изображен­ные справа, или структурированная запись, приведенная слева. Блок-схемы наглядны. Однако блок-схемы трудно рисовать, в них сложно вносить изменения и исправления из-за сложности перерисовки рамок и стрелок. Однако блок-схемы до сих пор требуются отечест­венными стандартами на документирование программ.

Достоинство записи алгоритмов и программ в структурирован­ной форме заключается в простоте их чтения и ввода с экрана ЭВМ, а также в простоте внесения изменений и исправлений с исполь­зованием даже самых простейших редакторов тестов. По этим при­чинам зарубежом блок-схемы уже давно не используются ни для документирования, ни для обучения, а все современные языки построены на принципах структурного программирования.

Приведем примеры описания алгоритма и программы в структу­рированной записи:

АлгоритмПрограмма

алг «приветствие» ' приветствие

нач сls

запрос («Ваше имя=», NN) input «Ваше имя=», NN$

вывод («Добрый день», NN) print «Добрый день», NN$

кон end

Алгоритм, приведенный слева, записан на псевдокоде. Псевдокод - это язык записи структурированных алгоритмов в качестве докумен­тации к программам для ЭВМ. Особенность псевдокода заключается в том, что описания на нем выполняются на родном языке — рус­ском, английском, украинском, казахском, немецком и т. п.

Программа, приведенная справа, записана на языке Бейсик - языке программирования персональных ЭВМ. Языками программи­рования называются формализованные языки, используемые для записи программ на ЭВМ. Одним из них является язык Бейсик.

Достоинства псевдокода заключаются в том, что описания алго­ритмов, записанные на родном языке, намного проще читать и по­нимать, чем запись программ на языке с иностранной лексикой. По этим причинам псевдокод используется как основное средство до­кументирования программ во всех ведущих фирмах, занимающихся разработкой программ.

С точки зрения информатики алгоритмы, записанные в такой обобщенной записи, позволяют выразить общую логику работы про­грамм, независимо от используемых языков программирования и типов ЭВМ. При этом алгоритмы, записанные в такой обобщенной форме, могут быть реализованы с помощью различных языков про­граммирования для самых различных типов ЭВМ.

В качестве примера приведем реализацию этого же диалогового алгоритма на самой ранней версии языка Бейсик, использовавшего­ся на самых первых персональных компьютерах:

АлгоритмПрограмма

алг «приветствие» 10 ' приветствие

нач 20 сls

запрос («Ваше имя=», NN) 30 input «Ваше имя=», NN$

вывод («Добрый день», NN) 40 print «Добрый день», NNS

кон 50 end

Основные свойства алгоритмов и программ для вычислительных машин - однозначность, результативность, правильность и массо­вость. Этими свойствами алгоритмы отличаются от различного рода расплывчатых и неоднозначных предписаний, инструкций и кули­нарных рецептов, которые могут толковаться и исполняться многими способами.

Однозначность алгоритмов - это однозначность правил их вы­полнения. Следствием этого свойства алгоритмов является однознач­ность результатов их выполнения в одинаковых начальных условиях. Это не всегда верно для кулинарных рецептов, когда разные испол­нители в одних и тех же условиях могут придавать различный вкус и пикантность одним и тем же блюдам.

Результативность - это завершение выполнения алгоритмов оп­ределенными результатами. Результативность - наиболее важное свойство алгоритмов и программ, предназначенных для решения при­кладных задач. Алгоритмы и программы, не дающие результатов или ведущие к сбоям и отказам, никому не нужны.

Массовость - это возможность применения алгоритмов в раз­личных конкретных исходных условиях. Массовые алгоритмы осо­бенно важны для решения прикладных задач, когда алгоритмы и программы должны обеспечить решение целого класса задач, разли­чающихся исходными данными.

Правильность алгоритмов определяется правильностью резуль­татов, получаемых с их помощью. По этой причине правильность алгоритмов и программ является относительным понятием. Оценка правильности может проводиться только при наличии требований к конечным результатам.

Алгоритм считается правильным, если он дает правильные резуль­таты для любых допустимых начальных условиях. Правильность алгоритмов гарантирует правильность результатов их выполнения.

Алгоритм содержит ошибки, если его выполнение может привести к отказам, сбоям или неправильным результатам, либо вовсе не дает никаких результатов. Эти ошибки называются алгоритмическими. Алгоритмы и программы, содержащие такие ошибки, могут нанести вред или ущерб тем, кто захочет ими воспользоваться.

Для оценки правильности алгоритмов и программ необходимо уметь оценивать результаты выполнения составляющих их действий и конечные результаты их выполнения в целом.

Простейшие виды машинных операций - операции присваивания. С помощью присваивании в алгоритмах описываются вычисления в программах для ЭВМ. Рассмотрим примеры операций присваива­ния и описания результатов их выполнения.

Присваивания: Результаты:

а:= 0 а = 0

b:= а + 1 b ' = а + 1 = 1

b:= b + 1 b " = b' + 1 = 2

 

Запись присваиваний читается:

а:= 0 - «переменной а присвоить значение 0»;

b:= b + 1 - «переменной b присвоить значение b + 1».

Записи в колонке результатов читаются так:

а = 0 - «значение а равно 0»;

b' = b + 1 - «значение b' равно b + 1».

 

Здесь а и b - программные переменные - область машинной па­мяти, в которой хранятся их значения а и b. В отличии от обычных математических переменных программные переменные могут полу­чать новые значения. В частности, присваивание b: = b + 1 запи­сывает в программную переменную b новое значение b', равное величине b + 1, где b - прежнее значение переменной b.

Для описания результатов выполнения алгоритмов и программ могут и должны использоваться спецификации. Спецификации - это точные, математически строгие описания. Примерами спецификаций могут служить сценарии диалоговых программ.

Сценарии диалоговых алгоритмов и программ - это совокупность текстов, картинок и сообщений, появляющихся на экранах ЭВМ. Рассмотрим в качестве примера сценарий алгоритма рисования домика на экране ЭВМ.

 

Сценарий «Домик»

 

 

Решение - следующие алгоритм и программа, результатом работы которых должен быть приведенный выше рисунок:

 

АлгоритмПрограмма

алг «Домик» ' Домик

нач screen 2,0

линия (130,40)-(100,100), красная line (150,40)-(100,100),8

линия (130,40)-(200,100), красная line (150,40)-(200,100),8

рамка(100,100)-(200,200), белая line (100,100)-(200,200),15,b

рамка(130,120)-(170,160), синяя line (130,120)-(170,160),3,b

кон end

Однако результатом выполнения приведенных алгоритма и про­граммы будет следующий рисунок:

Экран ЭВМ

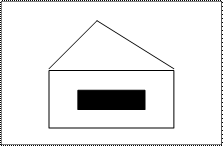Причиной того, что на этом рисунке крыша «поехала» влево, являются алгоритмические ошибки - неправильный расчет коорди­нат крыши в алгоритме, из-за чего составленная программа дает не тот рисунок, который указан в сценарии.

Примером прикладного алгоритма и программы может служить следующий алгоритм расчета прибыли:

Алгоритм Программа

алг «расчет прибыли» ' расчет прибыли

нач сls

запрос («доходы =», d) input «доходы =», d

запрос («расходы =», r) input «расходы =», r

р: = d - r р = d - r

вывод («прибыль =», р) print «прибыль =», р

кон end

Сценарий диалогаПротокол диалога

доходы =?<d> доходы =? 1000

расходы =? <г> расходы =? 700

прибыль = <р> прибыль = 300

Для проверки правильности алгоритма и программы необходима постановка задачи. Приведем строгую постановку решаемой задачи.

Задача: расчет прибыли.

Треб.: р - прибыль.

Дано: r - расходы;

d - доходы.

Где: d = r + р.

При: d > 0.

Для оценки правильности полученных результатов нужно сверить расходы и прибыль с доходами. В нашем случае это должно быть 700 + 300 = 1000, что выражает правильный конечный результат при указанных данных.

Для оценки правильности алгоритма и программы необходимо рассмотреть конечные результаты их выполнения при произвольных значениях данных d и г. Вычисляемая величина р по алгоритму будет равна

ОперацияРезультат

р:= d - r р = d – r

Подставляя в условие постановки задачи это значение, получаем:

d = r + p = r + (d - r) = d - верное тождество.

Таким образом, при любых значениях исходных данных результаты выполнения приведенного алгоритма будут правильными.

Поиск по сайту: