АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример простейшего линейного процесса

Читайте также:
  1. II звено эпидемического процесса – механизм передачи возбудителей.
  2. II. Принципы процесса
  3. VI. Педагогические технологии на основе эффективности управления и организации учебного процесса
  4. VII. По степени завершенности процесса воздействия на объекты защиты
  5. X. примерный перечень вопросов к итоговой аттестации
  6. АВТОМАТИЗАЦИЯ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
  7. Алгоритмизация процесса разработки и принятия управленческого решения
  8. Анализ деятельности Финской спортивной федерации по модели процесса эффективности функционирования
  9. Анализ качества продукции и производственного процесса
  10. Анализ технологии законодательного процесса в Тюменской области.
  11. Афферентный – понятие, характеризующее ход процесса нервного возбуждения по нервной системе в направлении от периферии тела к головному мозгу.
  12. Безопасность технологического процесса

Наиболее часто в практике программирования требуется организовать расчет некоторого арифметического выражения при различных исходных данных. Например, такого:

где x > 0 – вещественное, m – целое.

Разработка алгоритма обычно начинается с составления схемы. Продумывается оптимальная последовательность вычислений, при которой, например, отсутствуют повторения. При написании алгоритма рекомендуется переменным присваивать те же имена, которые фигурируют в заданном ариф­метическом выражении либо иллюстрируют их смысл.

Для того чтобы не было «длинных» операторов, исходное выражение полезно разбить на ряд более простых. В нашей задаче предлагается схема вычислений, представленная на рис. 1.1.

 

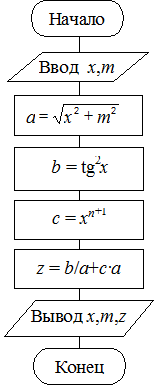
Рис. 1.1. Схема линейного процесса

 

Она содержит ввод и вывод исходных данных, линейный вычислительный процесс, вывод полученного результата. Заметим, что выражение вычисляется только один раз. Введя дополнительные переменные a, b, c, мы разбили сложное выражение на ряд более простых.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)