 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нелинейные структуры данных
В предыдущих разделах мы рассмотрели линейные структуры динамических списковых данных.
Введение в динамическую переменную двух и более полей-указателей позволяет получить нелинейные структуры данных. Наиболее распространенными являются структуры с иерархическим представлением, которые хорошо изображаются следующим образом:
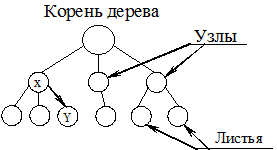
Такая конструкция данных получила название «дерево».
Дерево состоит из элементов, называемых узлами (вершинами). Узлы соединены между собой направленными дугами. В случае X ® Y вершина X называется родителем, а Y – сыном (дочерью).
Дерево имеет единственный узел, не имеющий родителей (ссылок на этот узел), который называется корнем. Любой другой узел имеет ровно одного родителя, т.е. на каждый узел дерева имеется ровно одна ссылка.
Узел, не имеющий сыновей, называется листом.
Внутренний узел – это узел, не являющийся ни листом, ни корнем. Порядок узла равен количеству его узлов-сыновей. Степень дерева – максимальный порядок его узлов. Высота (глубина) узла равна числу его родителей плюс один. Высота дерева – это наибольшая высота его узлов.
Поиск по сайту: