Умножение матрицы на вектор и матрицы на матрицу

Алгоритмы умножения матрицы на вектор и матрицы на матрицу реализуют основные операции матричной алгебры. Они достаточно просты, но очень наглядно иллюстрируют применение циклов при работе с массивами.

В результате умножения матрицы A состоящей из m строк и n столбцов на вектор X, со-держащий n компонентов, получается вектор Y, состоящий из m компонентов:

Y = A x X.

Каждый компонент результирующего вектора Y находится по формуле:

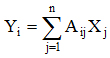; (i = 1, 2, 3, …, m)

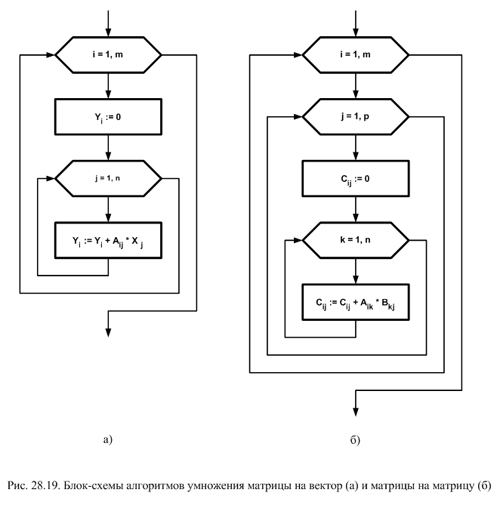
Из этой формулы следует внешний цикл по индексу i. В теле этого цикла происходит накопление суммы. Обычно специальной переменной для суммы не используют, а накапливают ее в i -том компоненте вектора Y. Перед накоплением суммы Y_i обнуляется, а затем организуется цикл по индексу суммирования j. Блок-схема этого алгоритма приведена на рис. 28.19 а.

В результате умножения матрицы A из m строк и n столбцов на матрицу B из n строк и p столбцов получается матрица C, состоящая из m строк и p столбцов:

C = A x B

Каждый элемент матрицы-результата рассчитывается по формуле:

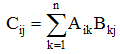(i = 1, 2, 3, …, m; j = 1, 2, 3, …, p)

Блок-схема алгоритма перемножения матриц приведена на рис. 28.19 б. Он очень похож на предыдущий, но только элементы результирующей матрицы рассчитываются в двойном цикле по индексу строки i и индексу столбца j. Накопление суммы выполняется в цикле по переменной k.

Поиск по сайту: