Вектор поляризации

Количественной характеристикой поляризации диэлектрика во внешнем электрическом поле является вектор поляризации. Рассмотрим диэлектрик, находящийся в электрическом поле (рис.27). Выделим внутри диэлектрика небольшой объем dV так, чтобы не нарушить внутреннего поля, и вместе с тем достаточно большой, чтобы он содержал значительное количество элементарных диполей. Пусть суммарный дипольный момент в объеме dV будет .Величина среднего дипольного момента единицы объема диэлектрика

(3.3)

характеризует поляризованность диэлектрика или интенсивность поляризации. Результирующий вектор , определяемый равенством (3.3), называется вектором электрической поляризации.

Электрический дипольный момент каждой отдельной молекулы пропорционален напряженности электрического поля. Это значит, что

. (3.4)

Здесь коэффициент пропорциональности κ отражает свойство диэлектрика поляризоваться в электрическом поле. Он получил название абсолютной диэлектрической восприимчивости. Величина называется относительной диэлектрической восприимчивостью.

Для полярных диэлектриков κ зависит от температуры, т. е. κ = κ(Т). Так как векторы и параллельны, то имеет место неравенство κ > 0. Только в анизотропных средах и некоторых кристаллах векторы и не совпадают по направлению. Диэлектрическая восприимчивость таких сред оказывается не скалярной величиной, а тензорной, т.е. зависит от направления вектора напряженности внешнего электрического поля по отношению к кристаллографическим осям симметрии кристалла.

3.3. Связь между вектором поляризации
и плотностью связанных зарядов

Если в диэлектрике дипольный момент атома или молекулы р_э = ql, а количество их в единице объема равно п, то дипольный момент единицы объема выразится так:

. (3.5)

Направление вектора поляризации для неполярных диэлектриков совпадает с направлением смещения зарядов. Но , тогда

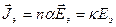. (3.6)

Отсюда

На торцевых поверхностях диэлектрика под влиянием внешнего электрического поля наводятся заряды с поверхнстной плотностью: ±σ΄ и с q΄ = σ΄ab (рис. 28). Результирующий дипольный момент в этом случае равен

. (3.7)

Отсюда вектор электрической поляризации однородного диэлектрика численно определится выражением

, (3.8)

так как то .

Если параллелепипед, изображенный на рис. 28, косой, то для σ' необходимо учитывать только нормальную составляющую вектора поляризации , т.е. , (3.9)

где - единичный вектор нормали.

Более наглядно внешнее и внутреннее поля в веществе изображены на рис. 29. До внесения диэлектрика между пластинами плоского конденсатора напряженность электрического внешнего поля равнялась . При внесении диэлектрика в поле он поляризуется и его связанные заряды создают поле 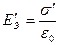(внутреннее поле в диэлектрике). Результирующая напряженность электрического поля внутри диэлектрика равна

. (3.10)

Но внутри плоского конденсатора в соответствии с (1.53) имеем . (3.11)

В свою очередь 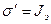. Тогда равенство (3.10) принимает вид

(3.12)

или в векторной форме

. (3.13)

Из (3.10) и (3.11) следует, что напряженность электрического поля внутри диэлектрика определяется как связанными, так и свободными зарядами, тогда как вектор электрического смещения 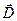- только свободными зарядами. Уравнение (3.13) можно представить еще и так:

, (3.14)

где , - плотность электрических зарядов, смещенных в свободном от молекул диэлектрика пространстве, т. е. в пустоте (вакууме).

Значит, можно говорить об электрическом смещении не только в диэлектрике, но и в свободном от вещества пространстве, хотя нельзя это наглядно описать. Следует иметь в виду, что в процессе разделения электрических зарядов создается электрическое поле, которое изменяется со временем. На всякое изменение электрического поля, обусловленное смещением электрических зарядов внутри диэлектрика, затрачивается работа. Изменяющееся со временем электрическое поле формирует электромагнитную волну, которая поглощается диэлектриком и частично выносится из зоны поляризации среды со скоростью света в окружающее пространство. Получается, что при внесении диэлектрика в электрическое поле должно происходить увеличение его температуры, и он является источником электромагнитных волн.

3.4. Связь диэлектрической проницаемости
с электрической восприимчивостью

Вектор электрической поляризации , а вектор электрического смещения . Учитывая это, равенство (3.13) можно записать иначе:

или (3.15)

Так как , то всегда больше ε₀ и

.

Отсюда

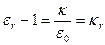или . (3.16)

Учтем, что

.

Тогда окончательно получаем:

. (3.17)

Следовательно, величина наведенных зарядов σ' тем больше, чем больше относительная диэлектрическая проницаемость среды ε_r.

Поиск по сайту: