Примеры решения задач. Решение задач по данной теме предполагает использование законов силового действия электрического поля при расчетах конкретных сил взаимодействия точечных

Решение задач по данной теме предполагает использование законов силового действия электрического поля при расчетах конкретных сил взаимодействия точечных зарядов и заряженных тел конечных размеров. Важным также является умение вычислять напряженность электрического поля, создаваемого точечными и заряженными телами на основании принципа суперпозиции и теоремы Остроградского-Гаусса. Рассмотрим некоторые примеры.

Пример 1. Три одинаковых заряда q расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре этого треугольника (рис. 15), чтобы результирующая сила, действующая на каждый заряд, была равна нулю?

Р е ш е н и е

При решении задачи используем принцип суперпозиции электрических полей и закон Кулона. На заряд q₂ действует заряд q₁ с силой

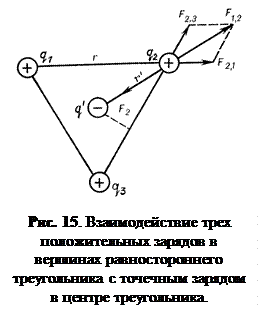
и заряд q₃ с силой

Из рис. 15 следует, что результирующая сила равна

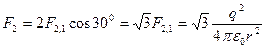. (1.61)

Ясно, что в центре треугольника необходимо поместить заряд противоположного знака. Сила взаимодействия точечных зарядов q' и q по закону Кулона равна

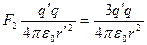. (1.62)

Приравнивая (1.61) и (1.62), окончательно получим

. (1.63)

О т в е т. В центре равностороннего треугольника необходимо поместить

заряд q' противоположного знака величиной .

Пример 2. Найти силу, действующую на точечный заряд q₁ = l,7∙10^-9 Кл, расположенный в центре полукольца, радиус которого r₀ = 5 см. По полукольцу равномерно распределен заряд Q = 3∙10^-7 Кл.

Р е ш е н и е

Так как полукольцо не является точечным зарядом, то для определения силы F использовать непосредственно закон Кулона нельзя. Нужно разбить полукольцо на элементарные участки dl с зарядом dQ (настолько малые, чтобы их можно было считать точечными) и по закону Кулона определить силу взаимодействия между двумя точечными зарядами q и dQ, находящимися на расстоянии r₀ (рис. 16):

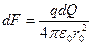
Учитывая, что , а , получим:

. (1,64)

При переходе от одного элемента полукольца к другому величина силы dF не изменяется, а меняется только направление. Поэтому следует найти проекции силы dF на оси x и y (dF_x = F sin α; dF_y = F cos α), а затем просуммировать. В результате имеем:

(1.65)

Следовательно, искомая сила взаимодействия заряженного полукольца с точечным зарядом q направлена по оси х и численно равна

. (1.66)

Подставляя числовые данные в системе СИ, получаем:

(1.67)

О т в е т: F = 1,15∙10^-3 Н.

Пример 3. Определить напряженность электрического поля внутри и вне равномерно заряженного длинного цилиндра с объемной плотностью заряда ρ. Радиус цилиндра r₀ и диэлектрическая проницаемость ε_r.

Р е ш е н и е:

Для решения этой задачи воспользуемся теоремой Остроградского-Гаусса. Выберем внутри цилиндра (рис. 17) замкнутую поверхность в виде цилиндра, радиус которого равен r, а длина – l. Поток вектора электрического смещения через выбранную поверхность определим по формуле

(1.68).

Из (1.68) следует, что и возрастают линейно с расстояния r до r = r₀.

Вне цилиндра, имеющего радиус r₀, поток вектора электрического смещения равен

(1.69)

Отсюда и уменьшаются, как 1/r. На границе цилиндра напряженность возрастает скачком в ε_r раз.

О т в е т: Внутри цилиндра напряженность электрического поля а вне цилиндра .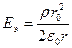

Поиск по сайту: