Энергия заряженного тела

Пусть на теле сосредоточен заряд q, который создает потенциал φ (рис. 21). Чтобы сообщить телу еще небольшой заряд dq, необходимо совершить работу, равную

. (2.15)

Полная работа по накоплению электрического заряда на изолированном теле определится так:

, (2.16)

а это есть энергия электрического поля заряженного тела.

Энергия электрического поля уединенного заряженного тела равна половине произведения электроемкости на квадрат потенциала.

2.5. Энергия поля конденсатора.
Плотность энергии электрического поля

На рис. 22 схематически показан заряженный плоский конденсатор. Внутри него образуется однородное электрическое поле напряженностью . Работа по разделению зарядов на обкладках конденсатора равна

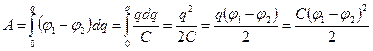. (2.17)

Следовательно, энергия электрического поля системы заряженных тел (конденсатора) равна половинному произведению электроемкости на квадрат разности потенциалов.

Используя зависимости и 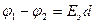для плоского конденсатора, получим следующее значение для энергии электрического поля, сосредоточенного внутри плоского конденсатора:

. (2.18)

В (2.18) произведение S·d есть объем, который занимает электрическое поле внутри конденсатора. Электрическое поле внутри плоского конденсатора однородное, и пренебрегая краевыми эффектами, получаем, что в единице объема будет содержаться следующее количество энергии:

Следовательно, плотность энергии электрического поля пропорциональна произведению вектора электрического смещения на напряженность электрического поля в заданной точке.

В случае неоднородного электрического поля его энергия определяется интегралом вида: . (2.20)

Используя понятия потенциала и электроемкости, возможно производить расчеты энергии электрического поля в самых разнообразных условиях его возникновения.

Поиск по сайту: