Закон Ома

При движении электромагнитной волны (электрического тока) по проводнику электрическое ноле Е_э у поверхности проводника имеет тангенциальную (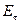) и нормальную (Е_п) составляющие. Составляющая 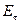обусловливает течение тока вдоль проводника и равна падению потенциала на единице длины . Составляющая , где σ -- плотность поверхностных зарядов. Полное поле . Как нормальная составляющая, так и тангенциальная составляющая связаны с магнитным полем, которое возникает вследствие протекания электрического тока. Тогда в соответствии с (5.22) и, учитывая взаимную перпендикулярность векторов Е_n и Н, получаем Е_n = v В и соответственно Е_τ = v В. Следовательно, вектора Е_n и Е_τ равны по абсолютному значению друг другу, а результирующий вектор электромагнитной волны по отношению к направлению распространения электромагнитной волны расположен под углом 45⁰.

Реально вектор Умова-Пойнтинга(9.8)состоит из двух частей:

. (9.11)

Первое слагаемое обозначим , второе и рассмотрим их порознь.

На рис. 105 изображено направление тангенциальной составляющей электрического поля , тока I и напряженности магнитного поля , которая направлена по касательной к силовой линии, замыкающейся вокруг тока.

Применяя правило буравчика (вращение от к ), находим, что вектор Умова-Пойнтинга направлен внутрьпроводника, перпендикулярно к его боковой поверхности. Из этого следует, что электромагнитная энергия непрерывно втекаетв проводник из окружающего пространства вследствие приложенного тангенциального внешнего электрического поля. Если внешнее поле отсутствует, то проводник является антенной, поглощающей электромагнитные волны из окружающей среды. Когда к проводнику приложено внешнее электрическое поле, то по проводнику распространяется электромагнитная волна, вектор Умова-Пойнтинга которой направлен внутрь проводника. Вследствие интенсивного поглощения на флуктуациях плотности, обусловленной кластерной структурой вещества, электромагнитная волна по мере распространения вдоль оси Х -ов уменьшается по интенсивности. Рассмотрим, какие при этом происходят количественные изменения.

Воспользуемся первым уравнением системы (9.3) и умножим его на dx. Тогда 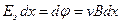. (9.12)

Для конечного проводника длиной l формула (9.12) примет вид:

.

С учетом (9.1) и значения магнитной индукции магнитного поля бесконечно длинного проводника получаем:

. (9.13)

Отсюда следует, что на концах проводника длиной l и радиуса r возникает разность потенциалов пропорциональная величине электрического тока. Коэффициент пропорциональности R характеризует способность проводника пропускать через себя электрический ток, и поэтому был назван электрическим сопротивлением проводника. Электрическое сопротивление проводника измеряется в Омах: 1 Ом = 1 В /1 А.

Исторически опытным путем было установлено, что сопротивление проводника пропорционально длине проводника и обратно пропорционально его площади сечения. Введя коэффициент пропорциональности, запишем эту связь в виде следующего соотношения:

. (9.14)

где S – площадь поперечного сечения проводника

Для проводника круглого сечения:

. (9.15)

Коэффициент пропорциональности получаем путем сравнения с (9.13), а именно: или 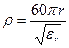. (9.16)

Здесь учтено, что для проводников . Величина ρ получила название удельного сопротивления проводника, обратная величина которой характеризует способность проводника проводить электрический ток, и названа электропроводностью.

Экспериментально зависимость (9.13) была установлена Омом в 1826 г. и названа законом Ома. Закон Ома гласит: величина электрического тока на выбранном участке электрической цепи прямо пропорциональна приложенному к этому участку цепи напряжению.

Закон Ома, записанный в форме (9.13), представляет собой интегральную запись этого закона. Чтобы выразить закон Ома в дифференциальной форме представим формулу (9.13) с учетом (9.14) в ином виде:

. (9.17)

Если поделить это равенство на площадь S, то выражение следует рассматривать как плотность тока. Сила электрического тока является скалярной величиной, а плотность тока – векторная величина и направлена вдоль нормали к площади S. В общем случае получаем следующую зависимость: . Тогда закон Ома (9.13) в интегральной форме запишется так:

, (9.18)

а в дифференциальной форме:

. (9.19)

Экспериментально было установлено, что удельное сопротивление зависит от температуры проводника и для металлов при обычных температурах имеет вид:

, (9.20)

где t - температура по шкале Цельсия; ρ_о - удельное сопротивление при а - температурный коэффициент.

Если температура измеряется по шкале Кельвина, то

, (9.21)

где Т - температура по абсолютной шкале. Это соотношение приближенное. При высоких температурах происходит рост удельного сопротивления относительно линейной зависимости, а при низких - резко падает, как показано на рис. 106. Электрические свойства твердых тел обусловлены поляризацией кластеров в металлах и ориентационной поляризацией в диэлектриках и керамиках. Ориентационная поляризация возникает вследствие преодоления диполь-дипольного взаимодействия встроенных электрических диполей взаимодействующих частиц. Зависимость удельного сопротивления от температуры остается не ясной.

Зависимость удельного сопротивления от температуры. Сверхпроводимость. Твердое тело формируется кластерной решеточной структурой, которая является однородной. В межкластерных пустотах находятся свободные частицы (атомы, молекулы, кластеры). Если свободные частицы обладают собственными колебательными частотами, то они ответственны за поглощение электромагнитных волн при их распространении в такой среде. Однородная структура электромагнитные волны практически не поглощает, а оказывает влияние только на скорость распространения волны своей диэлектрической проницаемостью. В общем случае электрический вектор электромагнитной волны представим в виде

(9.22)

Здесь k = 2π/λ – волновой вектор, ω – частота распространяющейся электромагнитной волны, Е_э,0 – амплитуда электрической составляющей волны.

Под действием такой волны валентные электроны атомов (молекул, кластеров) совершают вынужденные колебания по закону

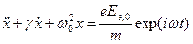, (9.23)

где m – масса колеблющейся частицы; ω₀ – собственная частота колебаний свободной частицы, на которую воздействует электромагнитная волна; γ – коэффициент затухания, который определяется временем жизни колеблющейся частицы и временем между двумя последовательными столкновениями.

Для отдельных свободных атомов частота собственных колебаний определяется резонансным переходом, а частота столкновений определяется временем между двумя последовательными столкновениями атомов внутри межкластерной пустоты. Например, для алюминия время жизни взбужденного состояния резонансного перехода составляет 3,3·10^-9 с, а время между двумя последовательными столкновениями при нормальной температуре – 1,0·10^-12 с. Следовательно, коэффициент затухания для алюминия при достаточно высоких температурах будет определяться в основном временем между двумя последовательными столкновениями. Аналогичная ситуация имеет место для всех металлов.

Для свободных атомных (молекулярных) систем смещением ядер при возмущении одного валентного электрона можно пренебречь и в свободном члене дифференциального уравнения (9.23) деление следует производить на массу одного электрона. В твердом теле такая ситуация имеет место для свободных атомов (молекул) в межкластерных пустотах. Таким образом, при распространении электромагнитной волны внутри твердого тела кластерная решеточная структура определяет скорость распространения волны, а свободные атомы в межкластерных пустотах определяют поглощение волны. Поглощение волны определяется законом Джоуля-Ленца.

Под действием вынуждающей силы (9.22) валентный электрон свободного атома совершает вынужденные колебания по закону

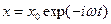, (9.24)

где амплитуда колебаний х₀ в соответствии с (9.23) определяется следующим образом:

. (9.25)

При отклонении валентного электрона от положения равновесия в атоме возникает наведенный дипольный электрический момент с амплитудой

. (9.26)

Полученный индуцированный электрический момент выражается через поляризуемость и напряженность электрического поля, т.е.

. (9.27)

Отсюда с учетом (9.26) получаем:

. (9.28)

Теперь воспользуемся формулой Клаузиуса-Моссоти и запишем ее в комплексном виде

, (9.29)

где n₀ – концентрация свободных атомов в межкластерных пустотах.

Комплексная диэлектрическая проницаемость выражается через комплексный показатель преломления

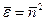, (9.30)

а комплексный показатель преломления представим в виде

, (9.31)

где действительная часть соответствует показателю преломления, а мнимая часть – главному показателю поглощения среды.

С учетом (9.30) и (9.31) уравнение Клаузиуса-Моссоти запишется так:

. (9.32)

Разделяя действительную и мнимую части выражения (9.32), получаем:

. (9.33)

Для металлов n² = ε_r >>1 и тогда система (9.33) с учетом того, что ω₀ >>ω, запишется так:

. (9.34)

Уравнение волны представим в комплексном виде иначе, т.е.

, (9.35)

или с учетом (9.24)

. (9.36)

Уравнение (9.36) описывает затухающую электромагнитную волну, где коэффициент затухания равен

. (9.37)

Интенсивность излучения электромагнитных волн пропорциональна квадрату напряженности электрического поля волны. Поэтому для интенсивности излучения коэффициент поглощения в два раза больше. Следовательно, поглощение определяется по интенсивности прошедшей волны, а это значит, что коэффициент поглощения для интенсивности составит:

. (9.38)

В уравнении Клаузиуса-Моссоти размерность поляризуемости равна м³/1частицу. Это значит, что полученный коэффициент поглощения соответствует одному монослою поглощающих частиц, а на единицу длины коэффициент поглощения равен

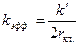, 1/м. (9.39)

Поток энергии внутрь проводника определяется вектором Умова-Пойнтинга с использованием тангенциальной составляющей. Мощность потока энергии внутри проводника длиной l круглого сечения на радиусе r составит

. (9.40)

Здесь Е_τ,0 – амплитудное значение тангенциальной составляющей электромагнитной волны.

Продифференцировав выражение (9.40) по r и взяв интеграл от начального радиуса r₀ до нуля, получим:

. (9.41)

Выражение (9.41) отражает закон Джоуля-Ленца. Учитывая это, получаем следующую формулу определения удельного сопротивления проводника круглого сечения

. (9.42)

Формула (9.42) отличается от (9.22) тем, что она еще содержит экспоненциальный член. Разложив в ряд экспоненциальный член и, ограничившись первым приближением, окончательно имеем

. (9.43)

Эффективный коэффициент поглощения линейно зависит от концентрации свободных атомов внутри межкластерных пустот. Для металлов в широкой области температур концентрация свободных атомов линейно зависит от температуры см. (9.20). Вблизи температуры плавления и выше начинает сказываться поглощение двухатомными молекулами в межкластерных пустотах, а по мере дальнейшего разогревания внутри межкластерных пустот образуются новые кластерные образования, что должно учитываться в коэффициенте поглощения, для которого линейная зависимость существенно нарушается.

При низких температурах граница между кластерами исчезает, образуется монолит, свободные атомы отсутствуют и в этих условиях коэффициент поглощения стремится к нулю. Относительная диэлектрическая постоянная стремится к единице. В результате для алюминия проводимость при температуре ~ 1K по отношению к проводимости при нормальной температуре возрастает на 7 порядков. Возникает сверхпроводимость для прохождения электромагнитных волн по проводнику вблизи абсолютного нуля температуры. Рассмотрим, как это происходит.

Вероятность образования монолита определяется энергией связи каждой частицы вещества с частицами третье координационной сферы и равна

. (9.44)

Здесь Е_св.3 – энергия бинарного взаимодействия частиц монолита с частицами третьей координационной сферы, которая для алюминия равна 2,30·10^-4 эВ, а f(E,T) – функция Максвелла-Больцмана. Если выразить энергию связи через температуру, то она соответствует 2,67 К. Расчет интеграла (9.44) в зависимости от температуры приведен на рис. 107. С учетом вероятности образования монолита получена проводимость алюминия при низких температурах. Значение критической температуры Т_С, при которой возникает сверхпроводимость, отмечено жирной линией на оси абсцисс. Надо полагать, что критическая температура соответствует увеличению свободных атомов в межкластерных объемах в е раз. Тогда для алюминия при Т_С = 1,178 К энергия связи должна соответствовать 1,9·10^-4 эВ. Отличие от расчетного значения энергии связи с атомами третьей координационной сферы составляет не более 20%, что вполне допустимо при выполненном достаточно грубом расчете.

Производить расчет для других веществ нет необходимости. Одного примера для обоснования физической природы возникновения сверхпроводимости вполне достаточно.

Явление резкого падения сопротивления впервые было открыто в 1911 г. Камерлинг-Онессом и называется сверхпроводимостью. Сверхпроводимость используется для создания постоянных во времени магнитных полей сравнительно большой величины. Мощные магнитные поля можно использовать для замагничевания плазмы, образующейся при сверхзвуковых полетах, в целях осуществления радиосвязи через плотную плазму, возникающую за ударной волной.

Удельное сопротивление пропорционально поперечному размеру проводника и обратно пропорционально корню квадратному из диэлектрической проницаемости. Поэтому в области температур, где диэлектрическая проницаемость существенно не изменяется с температурой, она возрастает линейно, т.к. линейно растет поперечный размер проводника. Опыт действительно дает линейную зависимость удельного сопротивления от температуры.

При высоких температурах меняется структура вещества, возникают фазовые переходы первого и второго рода. Это приводит к резкому уменьшению диэлектрической постоянной вещества и, соответственно, к росту удельного сопротивления проводника.

При температурах вблизи абсолютного нуля граница между кластерами в твердом теле исчезает, образуется однородный кристаллический монолит, в котором каждый атом связан с ближайшим окружением со значительной энергией связи. В результате нивелируются флуктуации плотности внутри проводника, что резко снижает поглощение электромагнитных волн, распространяющихся внутрь проводника. Возрастание энергии связи скачком приводит к резкому росту диэлектрической проницаемости и, соответственно, к быстрому падению удельного сопротивления проводника, т.е. возникает сверхпроводимость.

В тонких проводниках за счет сил поверхностного натяжения тоже образуется кристаллический монолит, а это значит, что для таких проводников должна возникать сверхпроводимость в очень высокотемпературной области. Это действительно имеет место при передаче электрического тока по тонкому проводу однопроводной линии сравнительно большой мощности.

Поиск по сайту: