АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Примеры решения задач. Решение задач по этой теме преследует цель закрепить основные навыки использования эффекта Холла и изменение сопротивления проводников и полупроводников для

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Решение логических задач средствами алгебры логики
  3. I. Розв’язати задачі
  4. I. Ситуационные задачи и тестовые задания.
  5. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  6. II. Основные задачи и функции
  7. II. Решение логических задач табличным способом
  8. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  9. II. Цель и задачи государственной политики в области развития инновационной системы
  10. III. Решение логических задач с помощью рассуждений
  11. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  12. IV. Определите, какую задачу взаимодействия с практическим психологом поставил перед собой клиент.

Решение задач по этой теме преследует цель закрепить основные навыки использования эффекта Холла и изменение сопротивления проводников и полупроводников для измерения напряженностей магнитных полей, а также каким образом гальваномагнитные и термомагнитные явления могут быть применены для изучения электрических свойств различных проводников и полупроводников.

 

Пример 1. Полупроводник в виде тонкой пластины шириной d = 1 cм и длиной l = 10 см помещен в однородное магнитное поле с индукцией В = 0,2 Т. Вектор индукции перпендикулярен плоскости пластины. К концам пластины (по направлению l) приложено постоянное напряжение U = 300 В. Определить холловскую разность потенциалов Ux на гранях пластины, если постоянная Холла Rx = 0,1 м3/К, удельное сопротивление ρ = 0,5 Ом·м.

 

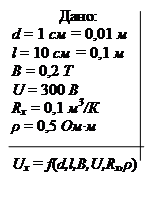Р е ш е н и е:

 

Холловская разность потенциалов определяется по формуле

 

В этой формуле неизвестна плотность электрического тока. В соответствии с законом Ома в дифференциальной форме

 

 

Пластину полупроводника можно представить как плоский конденсатор, для которого напряженность электрического поля с разностью потенциалов связана равенством

 

С учетом (13.39) и (13.40) равенство (13.38) запишется следующим образом

 

Все исходные данные представлены в системе СИ. Подставим эти значения в рабочую формулу (13.41) и произведем вычисления:

 

О т в е т: Ux = 1,2 B.

 

Пример 2. Магнитную индукцию измеряют холловским датчиком. Датчик изготовлен из иттербия, для которого коэффициент Холла составляет 35∙10-11 м3/Кл. Какую минимальную величину магнитной индукции можно измерить, используя датчик размером b · d · l = 1·10·10 мм, если на датчик подается напряжение 10 В. Удельное сопротивление иттербия 30∙10-6 Ом∙см. Регистрирующий усилитель постоянного тока позволяет измерять минимальное значение напряжения 1 мкВ.

Р е ш е н и е

 

Холловское напряжение определяется по формуле (13.1), а именно

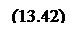
Отсюда

 

 

Плотность тока в соответствии с (9,18) равна

 

 

Подставив (13.43) в (13.42), получаем

 

 

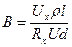
В (13.44) все величины известны. Подставим их значения и произведем вычисления

 

 

О т в е т: Минимальная величина магнитной индукции, которая может быть измерена данным холловским датчиком составляет 0,86 мТ.

 

Пример 3. Определить электропроводность электропроводящей керамики используя эффект Холла. Размер керамики b · d · l = 3·15·15 мм. К образцу приложено напряжение 200 В. Магнитная индукция внешнего магнитного поля 1 Т. Холловская разность потенциалов 0,6 В. Коэффициент Холла 1,05∙10-8 м3/Кл.

 

Р е ш е н и е:

 

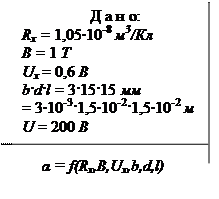Холловская разность потенциалов определяется формулой (13.1). Запишем эту формулу с учетом связи плотности тока с тангенциальной составляющей электрической напряженности, под действием которой возникает электрический ток.

 

Отсюда получаем:

 

Подставим значения величин в системе СИ и произведем вычисления

 

 

О т в е т: Электропроводность исследуемой керамики составляет 2,86∙105 Си (Сименса).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)