 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вынужденные электрические колебания
Вынужденные электрические колебания рассмотрим в двух вариантах, когда возбуждается последовательная электрическая цепь, и когда она представляет параллельную электрическую цепь. В первом случае реализуется резонанс напряжения, а во втором случае – резонанс токов.
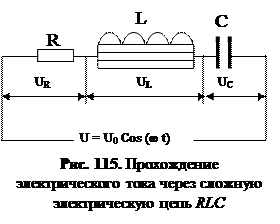 Конкретно рассмотрим последовательную электрическую цепь, изображенную на рис. 115, которая возбуждается переменным электрическим напряжением и состоит из активного сопротивления R, индуктивности L и емкости С. Сдвиг фаз между током и напряжением влияет на работу и мощность возбуждаемых электромагнитных колебаний в такой последовательной электрической цепи. С учетом этого замечания рассмотрим прохождение электромагнитных волн вдоль последовательной электрической цепи, изображенной на рис. 115.
Конкретно рассмотрим последовательную электрическую цепь, изображенную на рис. 115, которая возбуждается переменным электрическим напряжением и состоит из активного сопротивления R, индуктивности L и емкости С. Сдвиг фаз между током и напряжением влияет на работу и мощность возбуждаемых электромагнитных колебаний в такой последовательной электрической цепи. С учетом этого замечания рассмотрим прохождение электромагнитных волн вдоль последовательной электрической цепи, изображенной на рис. 115.
Результирующее напряжение равно сумме
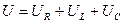 . (10.28)
. (10.28)
Для последовательной цепи величина электрического тока на всех элементах цепи является постоянной величиной и поэтому
 . (10.29)
. (10.29)
Отсюда с учетом формул (10.4) и (10.6) имеем: 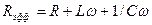 . Это было бы так, если не учитывать соотношение фаз между напряжениями различных элементов последовательной электрической цепи. Запишем уравнение (10.28), раскрыв все значения напряжений на каждом отдельном элементе цепи, следующим образом:
. Это было бы так, если не учитывать соотношение фаз между напряжениями различных элементов последовательной электрической цепи. Запишем уравнение (10.28), раскрыв все значения напряжений на каждом отдельном элементе цепи, следующим образом:  . (10.30)
. (10.30)
Поделим уравнение (10.30) на индуктивность L и запишем его в зарядовом представлении  . (10.31)
. (10.31)
Это обычное уравнение вынужденных колебаний, которое имеет вид:
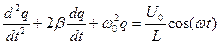 . (10.32)
. (10.32)
Найдем решение этого уравнения. Если прошло достаточно времени для установления колебаний, то, естественно, предположить, что установившиеся вынужденные колебания будут иметь периодический характер, постоянную амплитуду и частоту вынуждающего внешнего приложенного напряжения ω. Тогда решением уравнения (10.32) будет функция:
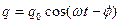 . (10.33)
. (10.33)
В этом уравнении амплитуда колебаний q0 и начальная фаза 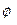 вынужденных колебаний должны быть как-то определены. Для нахождения этих величин возьмем первую и вторую производные от выражения (10.33) по времени
вынужденных колебаний должны быть как-то определены. Для нахождения этих величин возьмем первую и вторую производные от выражения (10.33) по времени
 (10.34)
(10.34)
Подставим эти выражения в уравнение (10.32) и в результате получим:
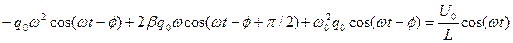 . (10.35)
. (10.35)
Поделим на 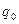 и приведем подобные члены
и приведем подобные члены
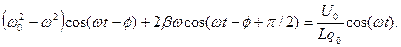
Введем обозначения:
 .
.
В этих обозначениях получаем:
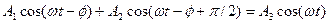 . (10.36)
. (10.36)
Правую часть выражения (10.36) следует рассматривать, как уравнение некоторого гармонического колебания, получившегося в результате сложения двух гармонических колебаний левой части этого равенства. Сложение колебаний осуществим путем применения метода векторных диаграмм.
 Проведем ось ОХ и отложим под углами, которые соответствуют начальным фазам всех трех колебаний, векторы
Проведем ось ОХ и отложим под углами, которые соответствуют начальным фазам всех трех колебаний, векторы 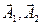 и
и  их амплитуд таким образом, чтобы
их амплитуд таким образом, чтобы 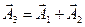 . Результирующая векторная диаграмма такого сложения приведена на рис. 116. Так как
. Результирующая векторная диаграмма такого сложения приведена на рис. 116. Так как  , то, подставив вместо
, то, подставив вместо 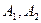 и
и  их значения, получим:
их значения, получим:
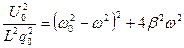 . (10.37)
. (10.37)
Из равенства (10.37) следует:
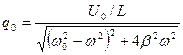 . (10.38)
. (10.38)
Приведенная на рис. 116 векторная диаграмма позволяет определять начальную фазу, введенную в (10.33), т.е.
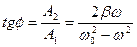 . (10.39)
. (10.39)
Исходя из первого уравнения (10.34), найдем величину установившегося электрического тока в цепи
 (10.40)
(10.40)
или в более компактном виде
 , (10.41)
, (10.41)
где 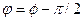 представляет собой сдвиг фаз между током и напряжением.
представляет собой сдвиг фаз между током и напряжением.
Из закона Ома для участка цепи падение напряжения на сопротивлении R составит: 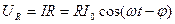 . (10.42)
. (10.42)
Напряжение на омическом сопротивлении изменяется в фазе с током.
Если второе равенство выражения (10.34) умножить на индуктивность, то получим ЭДС, которое генерируется на индуктивности L:
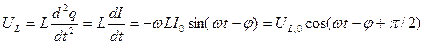 . (10.43)
. (10.43)
Получается, что напряжение на индуктивности опережает ток на  .
.
Если значение заряда, определяемое равенством (10.33), поделить на емкость конденсатора, то получим падение напряжения на емкости, а именно:
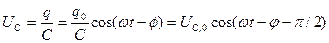 , (10.44)
, (10.44)
где 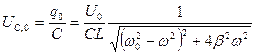 , а с учетом (10.13) и (10.25) получаем для определения амплитудного значения напряжения на емкости и начальной фазы формулы:
, а с учетом (10.13) и (10.25) получаем для определения амплитудного значения напряжения на емкости и начальной фазы формулы: 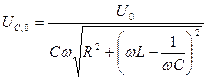 и
и 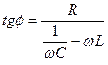 . (10.45)
. (10.45)
 На основании (10.44) напряжение на емкости отстает по фазе от силы тока на
На основании (10.44) напряжение на емкости отстает по фазе от силы тока на  , а по отношению к падению напряжения на индуктивности находится в противофазе. Общие фазовые соотношения для различных падений напряжений приведены на рис. 117. Выражения (10.38) и последующие (10.41)-(10.45) позволяют определять значения амплитуды тока, напряжения и начальной фазы вынужденных колебаний. Из них следует, что амплитуды тока и напряжения, а также начальная фаза зависят от соотношения между частотами ω и ω0. Колебания тока происходят не в фазе с колебаниями приложенного напряжения. Наибольшего значения электрический ток достигает не в тот момент, когда приложенное напряжение имеет максимальное значение.
, а по отношению к падению напряжения на индуктивности находится в противофазе. Общие фазовые соотношения для различных падений напряжений приведены на рис. 117. Выражения (10.38) и последующие (10.41)-(10.45) позволяют определять значения амплитуды тока, напряжения и начальной фазы вынужденных колебаний. Из них следует, что амплитуды тока и напряжения, а также начальная фаза зависят от соотношения между частотами ω и ω0. Колебания тока происходят не в фазе с колебаниями приложенного напряжения. Наибольшего значения электрический ток достигает не в тот момент, когда приложенное напряжение имеет максимальное значение.
Наибольший интерес представляет зависимость амплитуды тока и напряжения вынужденных колебаний от частоты приложенного напряжения и его величины при постоянной частоте собственных колебаний. Рассмотрим это явление подробнее.
Поиск по сайту: