Магнитное поле соленоида. Рассмотрим соленоид, имеющий длину l и радиус r0

Рассмотрим соленоид, имеющий длину l и радиус r₀. На единицу длины укладывается w₀ витков, по которым течет ток I (рис. 49). Участок соленоида длиной dl имеет w₀dl витков, и его можно рассматривать как круговой ток, равный

. (5.48)

Магнитная индукция в точке А на оси соленоида, создаваемая этим круговым током, определяется выражением

. (5.49)

Если учесть, что

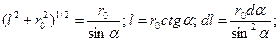
то 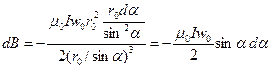. (5.50)

Результирующую магнитную индукцию найдем путем интегрирования:

. (5.51)

Внутри бесконечно длинного соленоида при отсчете углов по часовой стрелке имеем . Тогда

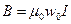(5.52)

и не зависит от местоположения точки, где определяется магнитная индукция. Это значит, что магнитное поле внутри соленоида однородно. На срезе бесконечно длинного соленоида и

. (5.53)

Индукция магнитного поля, создаваемого соленоидом, уже на его концах в два раза меньше, чем внутри, а вне соленоида она быстро падает. Следовательно, магнитное поле сосредоточено в основном внутри соленоида.

Поиск по сайту: