Резонанс напряжений в электрических цепях

Резонанс напряжений возникает в последовательной электрической цепи, изображенной на рис. 115. Амплитудное значение падения напряжения на электроемкости в последовательной RLC -цепи определяется по формуле (10.45). Из этой формулы определим отношение:

. (10.50)

Аналогичное отношение амплитудного значения падения напряжения на индуктивности к амплитудному значению напряжения источника питания на основании (10.43) равно:

. (10.51)

При резонансе и тогда . Учитывая это, получаем: 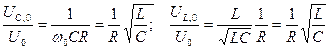. (10.52)

Следовательно, с учетом (10.27) имеем:

. (10.53)

Отсюда следует, что в резонансных условиях в последовательном RLC -контуре амплитудные значения падения напряжения на электроемкости и на индуктивности равны друг другу, а по отношению к амплитудному значению приложенного напряжения равны добротности контура. Добротность контура для многих колебательных систем представляет большую величину. Поэтому последовательный RLC -контур позволяет получать в резонансных условиях достаточно большие величины напряжения на электрической емкости. Такой резонанс является резонансом напряжения. Это свойство последовательного RLC -контура широко используется в технике. Например, люминесцентные лампы запитываются от электрической цепи путем применения последовательного RLC -контура. Возникающее при этом высокое напряжение на лампе приводит к пробою разрядного промежутка и, подчас, большой ее длины.

Поиск по сайту: