Электроемкость. Разделенные электрические заряды всегда связаны с какими-либо телами

Разделенные электрические заряды всегда связаны с какими-либо телами. Накапливать электрические заряды на том или ином теле можно не беспредельно. Каждое тело в зависимости от своей конфигурации способно накапливать только определенное, ограниченное количество электричества. Величина заряда, которая изменяет потенциал тела на 1 В, определяет электроемкость изолированного тела: 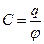. (2.7)

Электроемкость шара, радиус которого равен r₀, определяется выражением:

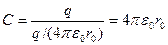. (2.8)

В системе СИ электроемкость измеряется в фарадах. Одна фарада - это электроемкость такого шара, который изменяет свой потенциал на 1 В, когда ему сообщают заряд в 1 Кл. Из (2.8) следует, что радиус такого шара r₀ = 1/4πε₀ = 9∙10⁹ м. Ясно, что электроемкость в 1 Ф – огромная величина. Поэтому на практике пользуются более мелкими единицами - микрофарадами (1 мкФ =10^-6 Ф) и пикофарадами (1 пФ = 10^-12 Ф). Например, для Земли электроемкость равна всего ~ 700 мкФ.

При наличии системы тел, образующих конденсатор, электроемкость определяется величиной заряда, которая изменяет разность потенциалов между телами на 1 В, т.е. 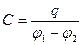. (2.9)

Для плоского конденсатора q = σ·S, аразность потенциалов в соответствии с (2.5) для однородного поля определяется соотношением: φ₁ – φ₂ =E_эd. Поскольку для плоского конденсатора Е_э=σ/ ε₀ ε_r [см. (1.48)], то

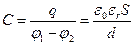, (2.10)

где d - расстояние между пластинами конденсатора.

Из (2.8) и (2.10) следует, что электроемкость зависит от размеров тел и их взаимного расположения. Чем больше размеры тела, тем больше его электроемкость. Чтобы обеспечить большое накопление электрических зарядов при сравнительно малых размерах, необходимо помещать тела в диэлектрики с большой относительной диэлектрической проницаемостью. Поэтому при производстве конденсаторов большой емкости и малых размерах используются сегнетоэлектрики, обладающие относительной диэлектрической проницаемостью 10⁴-10⁵.

Различные типы конденсаторов и их характеристики, используемые на практике приведены в табл. 2.1.

Если в качестве диэлектрика внутри плоского конденсатора использовать оксид иттрия Y₂O₃ толщиной 100 нм, напыленного в вакууме алюминием в несколько моноатомных слоев, то свернутая многослойная пленка высотой 20 см и диаметром 20 см будет обладать емкостью 56 Ф. Такая высокая емкость обусловлена тем, что молекулы Y₂O₃ обладаютбольшим встроенным электрическим моментом ~ 10 Дебая (3,33∙10^-29 Кл∙м). Таким образом, рассмотренная система представляет собой молекулярный конденсатор, созданный на наноуровне.

2.3. Электрическая энергия системы
электрических зарядов

При разделении двух точечных зарядов энергия взаимодействия

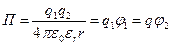, (2.11)

равна произведению заряда на потенциал в точке, где расположен этот заряд. Равенство (2.11) для одной пары зарядов можно представить и так:

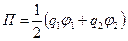. (2.12)

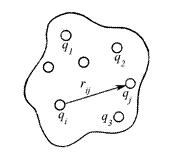
При наличии системы зарядов (рис. 20) энергия поля для каждой пары зарядов равна

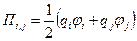. (2.13)

Взяв сумму всех возможных пар, получим общую энергию

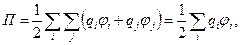(2.14)

которая отражает суперпозицию электрических полей.

Поиск по сайту: