Теорема Остроградского-Гаусса

На основании (1.42) определим поток вектора электрического смещения через любую замкнутую поверхность, внутри которой заключен точечный заряд q (рис. 10). В общем случае

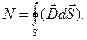(1.43)

На удалении r от точечного заряда , а проекция dS на направление нормали 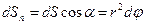, где 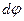— элемент телесного угла.

Значит,

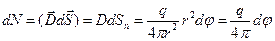, (1.44)

а полный поток равен

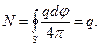(1.45)

Следовательно, поток вектора электрического смещения через любую замкнутую поверхность, внутри которой сосредоточен точечный заряд q, равен этому заряду:

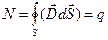(1.46)

Выражение ( 1.46 ) отражает теорему Остроградского-Гаусса. Из этой теоремы вытекают два следствия.

Следствие 1. Если замкнутая поверхность не охватывает заряда q, то

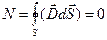(1.47)

Следствие 2. Если внутри замкнутой поверхности имеется множество зарядов 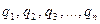, то

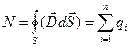(1.48)

Заряды суммируются каждый со своим знаком. Это обобщенная запись теоремы Остроградского-Гаусса, которая утверждает следующее: поток вектора электрического смещения через любую замкнутую поверхность равен алгебраической сумме заключенных в ней зарядов с учетом их знака.

Поток вектора электрического смещения измеряется в единицах заряда, т.е. в кулонах.

Теорема Остроградского-Гаусса используется для расчета электрических полей. Рассмотрим, например, поле заряженного шара, бесконечно заряженной плоскости и поле между двумя заряженными плоскостями.

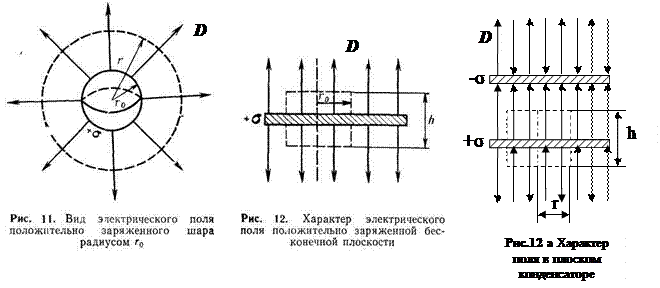В случае заряженного шара, имеющего радиус r₀ и поверхностную плотность зарядов 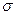, замкнутую поверхность выберем в виде сферы, радиус которой равен r (рис. 11). На поверхности S сферы вектор электрического смещения в силу сферической симметрии является постоянной величиной, а угол между нормалью к поверхности и вектором электрического смещения равен нулю. Тогда

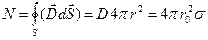(1.49)

Отсюда

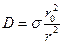и 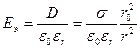(1.50)

Для бесконечно заряженной плоскости с поверхностной плотностью 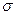замкнутую поверхность выберем, как показано на рис. 12, т. е. в виде цилиндра, имеющего радиус r₀ и высоту h. Поток вектора электрического смещения через боковую поверхность цилиндра равен нулю, а через торцевые поверхности

,

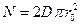так как имеются две торцевые поверхности - верхняя и нижняя. Применяя теорему Остроградского-Гаусса, получим

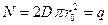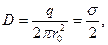или а 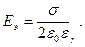(1.51)

Аналогично для двух бесконечно заряженных поверхностей разных знаков, формируемых плоский конденсатор, поток электрического смещения через выбранный цилиндр радиуса r обладает следующей величиной:

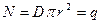. (1.52)

Отсюда:

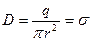и 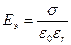(1.53)

Из рассмотренных примеров видно, что теорема Остроградского-Гаусса позволяет выбирать такую форму окружающих поверхностей, которая значительно облегчает расчет электрических полей, создаваемых любыми конфигурациями электрических зарядов.

Поиск по сайту: